brianslowsnai
- 3
- 0
Hi!,
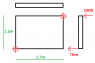
Im relatively new and need some help on a simple problem. If i have a force in one corner of an object and want a resultant bending moment in the opposite corner, how do i find this? see attached image.
Obviously i have two bending moments, 100Nx1.7m and 100Nx1.2m, how do I find a 'total' bending force in the resultant corner? - or can i take a diagonal length from the applied force to the reaction to find one bending moment?!
Thanks!
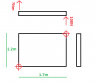
Im relatively new and need some help on a simple problem. If i have a force in one corner of an object and want a resultant bending moment in the opposite corner, how do i find this? see attached image.
Obviously i have two bending moments, 100Nx1.7m and 100Nx1.2m, how do I find a 'total' bending force in the resultant corner? - or can i take a diagonal length from the applied force to the reaction to find one bending moment?!
Thanks!