SUMMARY
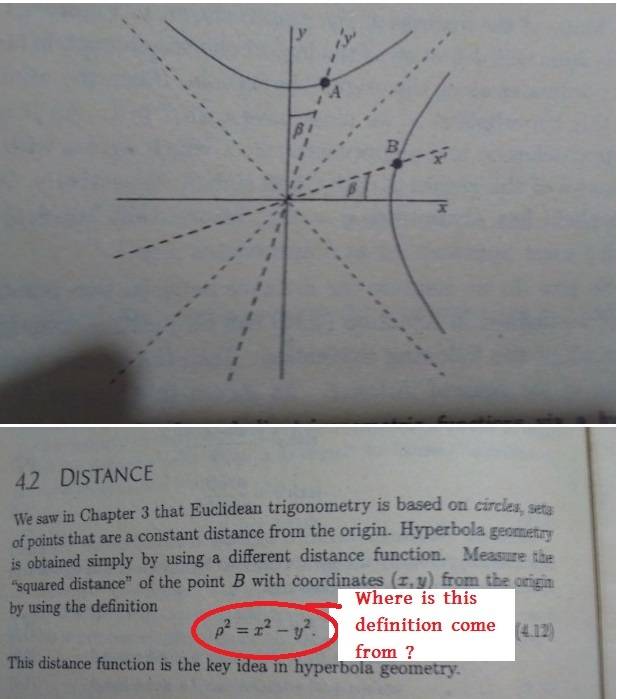
The distance formula for a hyperbola is derived from the definition of a hyperbola as the set of points where the difference in distances to two focal points is constant. Specifically, for a rectangular hyperbola defined by the equation ##x^2 - y^2 = \text{const}##, the derivation leads to the equation ##\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1##, where ##b = \sqrt{e^2 - a^2}##. The discussion emphasizes the mathematical perspective, avoiding physical interpretations such as Lorentz transformations. The concept of distance in hyperbolic geometry is distinct from Euclidean distance, as it relates to the hyperbola's structure.
PREREQUISITES
- Understanding of hyperbolic geometry and its definitions
- Familiarity with the Cartesian coordinate system
- Basic knowledge of algebraic manipulation and equations
- Concept of focal points in conic sections
NEXT STEPS
- Study the derivation of hyperbolic distance formulas in detail
- Explore the properties of hyperbolas in Cartesian coordinates
- Learn about the relationship between hyperbolic and Euclidean geometry
- Investigate applications of hyperbolic functions in various mathematical contexts
USEFUL FOR
Mathematicians, geometry enthusiasts, educators, and students seeking to deepen their understanding of hyperbolic geometry and its applications.