Discussion Overview
The discussion revolves around deriving the equation for the motion of a stone thrown vertically upward from a cliff, focusing on the mathematical modeling of its vertical displacement over time. Participants explore the implications of the model, including the significance of vertical versus horizontal displacement and the nature of the graph produced.
Discussion Character
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
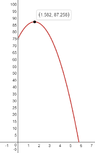
- One participant presents the equation for vertical displacement as \( f(t) = -\dfrac{1}{2}gt^{2} + v_{0}t + h_{0} \), emphasizing the importance of tracking signs and units.
- Another participant calculates the time to reach the highest point, arriving at approximately 1.582 seconds, but expresses uncertainty about the value of \( g \).
- Some participants clarify that the model refers only to vertical displacement, cautioning against misinterpretations related to horizontal motion.
- There is a discussion about the nature of the graph, with one participant asserting that the graph represents speed as a parabola, while others argue that it depicts vertical displacement over time.
- One participant suggests that observing the stone's motion from a fixed camera would not reveal a parabolic path, while another counters that the time axis is essential for defining the parabolic nature of the graph.
Areas of Agreement / Disagreement
Participants generally agree on the mathematical model for vertical displacement but disagree on the interpretation of the graph and the nature of the motion, with competing views on whether the graph represents speed or vertical displacement.
Contextual Notes
There are unresolved questions regarding the assumptions made about the motion, the interpretation of the graph, and the role of time in defining the parabolic nature of the trajectory.