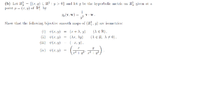How Do You Differentiate the Modulus of a Complex Number in Riemannian Metrics?

[Poirot1]

I'm interested in part iv) on the attachment. This is my work so far:
e=(1,0) and e'=(0,1) form a basis of the tangent space at any point z=(x,y). Making the identification (x,y)->x+iy, we get g(e,e')=0 and g(e,e)=g(e',e')=$\frac{1}{im(z)^2}$.

a(t)=z+t and b(t)=z+it are generating curves for e,e' respectively.
(lets call the function f)

$f(z)=\frac{z}{|z|^2}$ so $f(a(t))=\frac{z+t}{|z+t|^2}$. I need to find f'(a(t)) to proceed. How can I cope with differentiating the modulus of a complex number z? Thanks

 

[alyafey22]

Re: riemannian metric question

I don't know about metric spaces , but I know about complex analysis ... To differentiate a function a necessary requirement is to satisfy the cauchy-riemann equation .. suppose that $$f(z)=|z|$$ this function is clearly not differentiable

$$f(z)=\sqrt{x^2+y^2} $$

By the cauchy-reimann equation we must have $$\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y}$$

Which is clearly not satisfied for $$|z|$$

The function you are trying to differentiate seems a function of several variables ? , are you differentiating with respect to t ?

 

[Poirot1]

Re: riemannian metric question

I need to find the differential of f at z evaluated at e (and e'). This is equal to f'(a(t)) evaluated at t=0.