Discussion Overview
The discussion revolves around the representation of spacetime diagrams in the context of Minkowski spacetime, particularly focusing on the geometric and mathematical aspects of depicting four-dimensional spacetime in a three-dimensional framework. Participants explore the implications of velocity components in spacetime and the terminology used to describe angles and orthogonality in this context.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- Some participants assert that Minkowski spacetime is a four-dimensional continuum with mutually orthogonal axes, while others challenge the implications of this regarding the direction of motion through space and time.
- There is a debate about the representation of four dimensions in three-dimensional space, with some arguing that it is impossible to do so accurately.
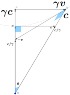
- Participants discuss the nature of angles in Minkowski space, with some suggesting that the term "right angle" is inappropriate and proposing the use of "orthogonal" instead.
- One participant emphasizes that the four-velocity is a four-dimensional vector that cannot be orthogonal to the time axis, while others provide conditions under which certain components may be perpendicular.
- There are differing views on how to depict spacetime diagrams, with some suggesting the use of a single four-vector rather than multiple vectors to represent velocities through space and time.
- Mathematical relationships involving rapidity and hyperbolic functions are introduced as part of the discussion on how to accurately represent spacetime diagrams.
Areas of Agreement / Disagreement
Participants express multiple competing views regarding the representation of spacetime diagrams and the terminology used to describe the relationships between space and time. There is no consensus on the best approach to depict these concepts or the appropriate mathematical framework to use.
Contextual Notes
Some statements rely on specific interpretations of velocity components and the definitions of angles in Minkowski space, which may not be universally accepted. The discussion also highlights the complexity of visualizing four-dimensional spacetime in a three-dimensional context.