evinda said:
But the vectors will only span the parallepiped since they have a common starting point, right?
Well, it's not that they have
any ol' starting point. You need the three vectors that exactly lie along three linearly independent edges of the parallelepiped (ppd for short). So, for a ppd, as long as you don't have two vectors that are pointed in the same or opposite direction, then any three such vectors will do.
If it's not the case that we get the same result no matter which way we do it, then the volume of the ppd is not well-defined. Is it this volume, or that volume?
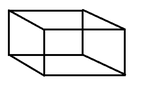
Well, let's say we have four vectors from the origin to vertices on the ppd. We want to use these vectors, or differences between them, to obtain three linearly independent vectors that exactly lie along three edges of the ppd. There are exactly twelve edges of a ppd, and they will be grouped in three classes by how they are parallel. So I think you can convince yourself that so long as the four vertices you have are such that there is one of them directly connected to the other three along an edge of the ppd, and you use that central point as the common subtrahend, you'll get three correct vectors.
The more challenging notion is that the vector triple product gives you the same result (in magnitude), no matter how you perform it. Suppose our three vectors are $\vec{a}, \vec{b},$ and $\vec{c}$. Then we're interested in the magnitude of the triple product: $|\vec{a}\cdot(\vec{b}\times
\vec{c})|$. As the wiki points out, this is equivalent to the determinant of the matrix formed by stuffing the elements of $\vec{a}$ along the first row, $\vec{b}$ along the second, and $\vec{c}$ along the third. Since swapping rows corresponds to doing a different version of the triple product, and swapping rows merely reverse the sign of the determinant, and since we're taking the magnitude of said determinant, I conclude that we can do any triple product we wish, and still get the correct answer.
It will be of the following form, right?
Looks good!
Which could be the given vertices?
As I mentioned above, you just need one of the vertices to be connected to the other three along edges of the ppd, and then you should use that vertex as the common subtrahend when you do your subtractions. That'll get you three vectors along edges of the ppd.