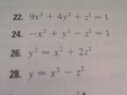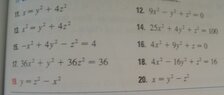ineedhelpnow
- 649
- 0
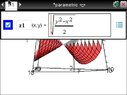
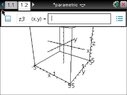
ok so this is the part I am really struggling with. we need to be able to recognize an ellipsoid, cone, elliptic paraboloid, hyprboloid of one sheet, hyperbolic paraboloid, hyperboloid of two sheets given an equation. he's going to give us an equation of one and ask us to identify and sketch the graph. please help me! and i would reaaaalllly appreciate it if anyone can let me know if they know how to graph these type of graphs on the ti nspire.
here are just some random examples of what we'll be asked on the test.
View attachment 3219View attachment 3216View attachment 3217View attachment 3218
here are just some random examples of what we'll be asked on the test.
View attachment 3219View attachment 3216View attachment 3217View attachment 3218
Attachments
Last edited: