Darkmisc
- 222
- 31
- Homework Statement
- z^3+8i=0
- Relevant Equations
- r^3cis3t = 8cis(-pi/2)
Hi everyone
How do you know how many solutions z has
a) in this problem
b) in general?
I understand that they are rotating 2 pi from (-pi/2) in both directions to get the other two solutions. Should this be done in all problems?
Is it simply a coincidence that there are three solutions when z is in the third power?
If the problem needed to be solved for z^4, would there be four solutions? Or only three (again by rotating 2 pi in both directions)? Thanks
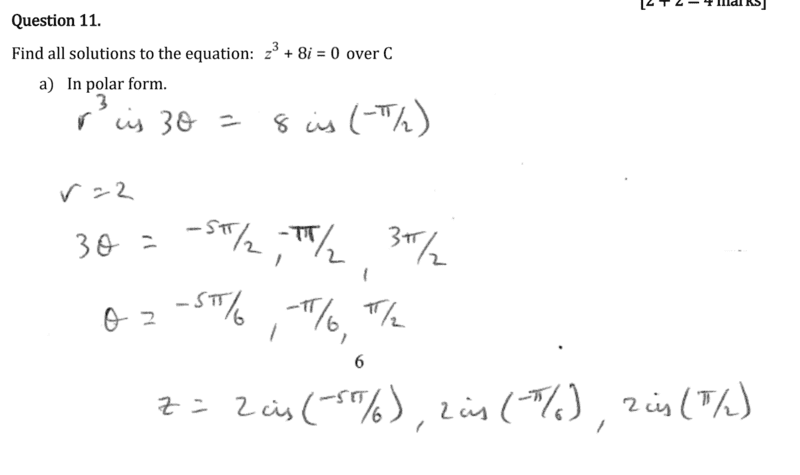
How do you know how many solutions z has
a) in this problem
b) in general?
I understand that they are rotating 2 pi from (-pi/2) in both directions to get the other two solutions. Should this be done in all problems?
Is it simply a coincidence that there are three solutions when z is in the third power?
If the problem needed to be solved for z^4, would there be four solutions? Or only three (again by rotating 2 pi in both directions)? Thanks
