How Do You Model the Changing Concentration of Nitric Acid in a Tank?

In summary: This gives $$\frac{d(VF)}{dt}=-8F+1.2$$ We can solve this separable differential equation to get $$F(t)=0.3-0.295e^{-8t}$$ To find when the percentage of nitric acid in the tank reaches 10%, we set F(t) = 0.1 and solve for t. This gives t = 0.056 minutes or approximately 3.36 seconds. So in summary, after t minutes, the volume of nitric acid in the tank is given by F(t) = 0.3-0.295e^{-8t} and the percentage of nitric acid in the tank
  • #1
Tapias5000
46
10
Summary:: A nitric acid solution enters at a constant rate of 6 liters / minute into a large tank that originally contained 200 liters of a 0.5% nitric acid solution. The solution inside the tank is kept well stirred and leaves the tank at a rate of 8 liters / minute. If the solution entering the tank has 20% nitric acid, determine the volume of nitric acid in the tank after t minutes. When will the percentage of nitric acid in the tank reach 10%?

A nitric acid solution enters at a constant rate of 6 liters / minute into a large tank that originally contained 200 liters of a 0.5% nitric acid solution. The solution inside the tank is kept well stirred and leaves the tank at a rate of 8 liters / minute. If the solution entering the tank has 20% nitric acid, determine the volume of nitric acid in the tank after t minutes. When will the percentage of nitric acid in the tank reach 10%?

How do I solve the 10% question I got this far.
aaaaaaaaaaaaaaaa.png


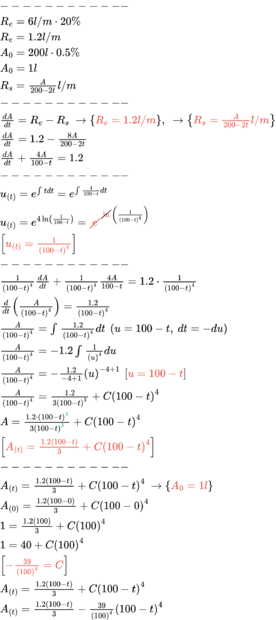
[Moderator's note: moved from a technical forum.]
 
Last edited by a moderator:
Physics news on Phys.org
  • #2
What's "edo"?
Code: 
Acronym	Definition
EDO	Extended Data Out (RAM)
EDO	Eating Disorder
EDO	Extended Data Output
EDO	Engineering Distributed Object
EDO	Event Delivery Object
EDO	Executive District Officer (Pakistan)
EDO	Economic Development Officer
EDO	Extended Duration Orbiter
EDO	Extra Day(s) Off
EDO	Engineering Duty Officer
EDO	Eastern District Office (various organizations)
EDO	Electronic Door Opener (various companies)
EDO	Electronic Distribution Only (US Marine Corps)
EDO	Education Development Officer (job title)
EDO	Earned Day Off (Canadian federal government)
EDO	Enlisted Dining Out (US Air Force)
EDO	Écurie de Dressage Orbecoise (French equestrian association)
EDO	Ethadione (medication)
EDO	Education Development Organization
EDO	Estate Duty Office (United Kingdom)
EDO	Emergency Detention Order (court order for mental health evaluation)
EDO	Engineering Duty Only (US Navy)
EDO	Engineering Data Center
EDO	Employer Deduction Order
EDO	Earl Dodge Osborne (EDO Corporation)
EDO	Electric Drive Option
EDO	Environmental Development Office
EDO	Expeditionary Decisive Operations
EDO	Exploratory Development Objective
EDO	Engineering Design Outsourcing
https://acronyms.thefreedictionary.com/EDO
 
  • Like
Likes vela
  • #4
I'd like to see your derivation of the equations. Here is my derivation: I think you are supposed to assume the percentage nitric acid is the volume percentage and that the solution overall density doesn't change. So, based on this, the volume of fluid in the tank is V = 200-2t, the amount of nitric acid in the tank at any time is FV, the rate of nitric acid entering is (6)(0.2), and the rate of nitric acid leaving at any time is 8F, where F is the fraction nitric acid in the tank at any time. So my nitric acid balance o the tank is $$\frac{d(VF)}{dt}=(6)(0.2)-8F$$ The initial condition is F = 0.005
 

FAQ: How Do You Model the Changing Concentration of Nitric Acid in a Tank?

How do I approach solving an application problem in EDO?

When solving an application problem in EDO, it is important to first understand the given problem and identify the variables and constants involved. Then, you can use the appropriate techniques, such as separation of variables or substitution, to solve the differential equation and find the solution.

What are some common techniques used to solve application problems in EDO?

Some common techniques used to solve application problems in EDO include separation of variables, substitution, and the method of undetermined coefficients. It is important to choose the appropriate technique based on the given problem and the type of differential equation.

How can I check if my solution to an application problem in EDO is correct?

To check if your solution to an application problem in EDO is correct, you can substitute the solution into the original differential equation and see if it satisfies the equation. Additionally, you can compare your solution to the given initial conditions to ensure that it satisfies them as well.

Can I use a calculator or computer to solve application problems in EDO?

While it is possible to use a calculator or computer to solve application problems in EDO, it is important to have a thorough understanding of the concepts and techniques used. Relying solely on a calculator or computer may lead to incorrect solutions or a lack of understanding of the problem.

Are there any tips for solving application problems in EDO more efficiently?

To solve application problems in EDO more efficiently, it is helpful to practice solving different types of problems and familiarize yourself with the techniques used. It is also important to carefully read and understand the given problem, and to check your solution for errors. Additionally, breaking the problem down into smaller steps and organizing your work can help make the process more efficient.

Similar threads

Linear Algebra System of Equations/Rates Application Help
Replies
1
Views
1K
Solving a Differential Equation: Salt Concentration in a Tank
Replies
1
Views
2K
Differential Equation Water Tank Word Problem
Replies
7
Views
4K
Acid Solution Tank Differential Equation: Determining Volume of Acid Over Time
Replies
1
Views
2K
Concentration of salt in the tank
Replies
1
Views
2K
Differential Equation (Water/Solution Tank) problem
Replies
1
Views
6K
Solution pumped into a tank problem.
Replies
16
Views
3K
Tank-Modeling Problem: Solving for Salt Amount with Differential Equations
Replies
1
Views
2K
Water Tank Differential Equation Problem
Replies
3
Views
7K
Modeling with First Order Differential Equation
Replies
11
Views
8K

Hot Threads

Recent Insights

Back
Top