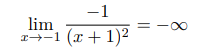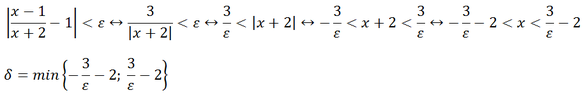To prove limits at infinity, the discussion focuses on two specific limits: the first, $$\lim_{x\to\infty}\frac{x-1}{x+2} = 1$$, requires demonstrating that for any $\varepsilon > 0$, there exists an $N$ such that $$\left|\frac{x-1}{x+2} - 1\right| < \varepsilon$$ for $x > N$. The second limit, $$\lim_{x\to-1}\frac{-1}{(x+1)^2} = -\infty$$, involves showing that for any $M$, a $\delta > 0$ can be found such that $$\frac{-1}{(x+1)^2} < -M$$ when $|x+1| < \delta$. The conversation emphasizes the importance of simplifying expressions and finding appropriate bounds for $N$ and $\delta$. Ultimately, understanding these definitions and calculations is crucial for proving limits at infinity effectively.