SUMMARY
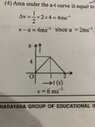
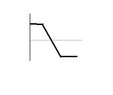
The discussion centers on the relationship between acceleration and velocity in one-dimensional motion, specifically addressing the calculation of velocity when acceleration is present. Participants clarify that the area under the acceleration-time graph represents the change in velocity, emphasizing that if the area is zero, the velocity remains constant. The conversation highlights that even when acceleration varies, as long as it remains positive, the velocity will continue to increase, albeit at a decreasing rate. The importance of understanding the graphical representation of acceleration and its impact on velocity is also underscored.
PREREQUISITES
- Understanding of kinematic equations in physics
- Familiarity with acceleration and velocity concepts
- Ability to interpret graphs of acceleration versus time
- Knowledge of the relationship between area under a curve and physical quantities
NEXT STEPS
- Study the kinematic equations for uniformly accelerated motion
- Learn how to derive velocity from acceleration graphs
- Explore examples of varying acceleration and its effects on velocity
- Investigate the implications of zero area under an acceleration-time graph
USEFUL FOR
Students of physics, educators teaching kinematics, and anyone interested in understanding the dynamics of motion in one dimension.