How Does Constant Acceleration Affect Antelope Speed Over 70 Meters?

[karush]

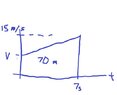
An antelope moving with constant acceleration covers the
distance between two points $\textbf{70.0m}$ apart in $\textbf{7.00s}$
Its speed as it passes the second point is $\textbf{15.00 m/s}$.
What is its speed at the first point?

The answer to this is 5 m/s

ok this should be real simple but kinda ?

$\displaystyle
\frac{70m}{7s}=\frac{10m}{s}$
so
$\displaystyle\frac{15-5}{2}=10\\
x=5$.

b. What is its acceleration

$\begin{align*}\displaystyle
a&=\frac{v_2-v_1}{t_2-t_1}\\
&=\frac{15-x}{7}\\
&\approx 1.43 m/s
\end{align*}$

kinda got it

suggestions?

 

[skeeter]

kinematics equation for constant acceleration ...

$\Delta x = \bar{v} \cdot t$

$\Delta x = \dfrac{v_0+v_f}{2} \cdot t$

solve for $v_0$, then $a = \dfrac{\Delta v}{t}$

 

[karush]

ok, I don't think I know what that would look with numbers given?

 

[skeeter]

ok, I don't think I know what that would look with numbers given?

Sorry, but I don't understand what you mean by that statement ... physics problems are solved using variables, then values are substituted as the last step.

$\Delta x = \dfrac{v_0+v_f}{2} \cdot t \implies v_0 = \dfrac{2\Delta x}{t} - v_f$

now substitute in your given values ... $v_f = 15 \, m/s$, $t = 7 \, s$, and $\Delta x = 70 \, m$

$v_0 = \dfrac{2 \cdot 70 \, m}{7 \, s} - 15 \, m/s = 5 \, m/s$

finally ...

$a = \dfrac{\Delta v}{t} = \dfrac{v_f-v_0}{t} = \dfrac{15 \, m/s - 5 \, m/s}{7 \, s} = \dfrac{10}{7} \, m/s^2$

 

[HallsofIvy]

A slightly different way of looking at it. With constant acceleration a, initial speed [math]v_0[/math], initial position [math]x_0[/math], [math]v(t)= at+ v_0[/math] and [math]x(t)= x_0+ v_0t+ (a/2)t^2[/math].

Taking the first point to be [math]x_0= 0[/math], [math]x(7)= 7v_0+ (49/2)a= 70[/math] and [math]v(7)= 7a+ v_0= 15[/math]. Since we only want to determine [math]v_0[/math], multiply the second equation by 7/2 to get the same coefficient of a, (49/2)a+ (7/2)v_0= 105/2, and subtract from the first equation: [math](7- 7/2)v_0= (7/2)v_0= 70- 105/2= 35/2[/math] so [math]v_0= 35/7= 5[/math] m/s.

Put [math]v_0= 5[/math] into either of those equations and solve for a: The simpler is [math]7(5)+ v_0= 35+ v_0= 15[/math] so [math]v_0= 15- 35= -25 m/s^2[/math]. This is negative indicating that the antelope was slowing down.

 

[RLBrown]

Plot velocity versus time.
The Area under the curve is the distance traveled for a given time interval.

View attachment 7670

Using the formula for volume of a trapezoid...

A =h (a+b)/2

Where:
a=v
b=15 m/s
h=7 s
A=70 m

then

70=7(v+15)/2
140/7=v+15
v=20-15=5