How Does Current Flow Through a 9V Battery in Different Circuit Configurations?

[deenuh20]

Homework Statement

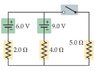
Two batteries and three resistors are connected as shown in the figure. How much current flows through the 9.0 V battery?

(a) When the switch is closed?
(b) When the switch is open?

Homework Equations

Kirchhoff's Loop Rule
I=V/R

The Attempt at a Solution

To find the current when the circuit is open, I totally disregarded the 5 ohm resistor and found the equivalent resistors of 2 and 4 and got 6. Then I used the equation I=9V/6 and that didn't work.

For the current when the circuit is closed, I applied Kirchhoff's Loop rule and found the current for each loop then solved by adding the two. That didn't work so I redrew the diagram and placed the 5 ohm resistor between the 2 and 4 ohm resistor and tried to figure out the current of that loop, but it also didn't work.

Additionally, does the 6 V battery in the drawing have anything to do with achieving the correct answer?

Thank you very much.

 

[deenuh20]

I was able to figure out the current for the open circuit, and it turned out to be 0.5 A. However, I'm still having trouble getting the answer for the closed circuit.

 

[SGT]

I was able to figure out the current for the open circuit, and it turned out to be 0.5 A. However, I'm still having trouble getting the answer for the closed circuit.

Show your work in order to get help.

 

[deenuh20]

For the open circuit, I found it to by 0.5A by taking the voltage/resistance, which was 6/(2+4)=1 A. Then, because the 2 ohm and 4 ohm resistors are parallel to each other, I divided 1 A by 2 and got 0.5A as my answer for the open circuit.

For the closed circuit, I applied Kirchhoff's rule. Because there was a junction right above the 9V, I found the current of the left square, which was 6V/(4ohm+2ohm)=1 A. Then, for the right square, I found the current of that loop to be 6V/(4 ohm + 5 ohm)=0.6667 A.

Then, because of Kirchhoff's junction rule, I1-I2-I3=0, so, I did 1-0.6667-I3=0 and solved for I3, which turned out to be 0.3333 A. I got this answer as the current going through the 9V battery in the closed circuit, but it is not working.

 

[SGT]

For the open circuit, I found it to by 0.5A by taking the voltage/resistance, which was 6/(2+4)=1 A. Then, because the 2 ohm and 4 ohm resistors are parallel to each other, I divided 1 A by 2 and got 0.5A as my answer for the open circuit.

You got the right answer with a faulty reasoning. The 2 ohm and 4 ohm are in series and not in parallel.
When applying KVL to the loop you must take into account both voltage sources and add them algebrically.

For the closed circuit, I applied Kirchhoff's rule. Because there was a junction right above the 9V, I found the current of the left square, which was 6V/(4ohm+2ohm)=1 A. Then, for the right square, I found the current of that loop to be 6V/(4 ohm + 5 ohm)=0.6667 A.

Then, because of Kirchhoff's junction rule, I1-I2-I3=0, so, I did 1-0.6667-I3=0 and solved for I3, which turned out to be 0.3333 A. I got this answer as the current going through the 9V battery in the closed circuit, but it is not working.

Again, your reasoning is faulty. You must take into account both voltage sources and remember that the 4 ohm resistor belongs to both loops, so there are two currents traversing it.