How does the row picture differ from the column picture in linear systems?

[otownsend]

Hi,

I hope someone can help. I'm wanting to get a better grasp on the connection between the row picture v.s. the column picture of linear systems and their solutions. In the picture below, the row picture are the three graphs on the top and their corresponding column pictures are below them:

View attachment 7384

Clearly there is a pattern here in terms of what to expect the linear system of equations to look like graphically when it is represented in row form v.s. column form.

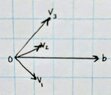
What I would like help on is the how a column picture like the one below would be represented as a row picture (sorry for it being a bit fuzzy):

View attachment 7386

I know that this solution exists and that there are infinite solutions, however I have no clue how this would be represented in the form of a column picture. I hope this makes sense.

If someone could explain this while also mentioning how this relates to linear independence and dependence that would be great.

 

[I like Serena]

Hi otownsend! Welcome to MHB!

In the row graph the intersection has coordinates x and y.
That corresponds to the column graph where $\mathbf b$ is a linear combination of $\mathbf a_1$ and $\mathbf a_2$ with factors x respectively y.

If we have a unique solution, the lines in the row graph intersect, and $\mathbf a_1$ and $\mathbf a_2$ are independent in the column graph, so that they can construct $\mathbf b$.

If there is no solution, either the lines in the row graph are parallel and do not coincide, or one of the equations does not have a solution at all, meaning it has no graph.
And $\mathbf a_1$ and $\mathbf a_2$ are on the same line while $\mathbf b$ is not on that line, meaning it can't be constructed, or one of $\mathbf a_1$ and $\mathbf a_2$ is zero, while $\mathbf b$ is not.

If there are infinitely many solutions, we can have coinciding lines, or one of the equations has infinitely many solutions, while the other has at least 1 solution.
I'll leave it up to you to figure out what that means for the columns graph. (Wink)