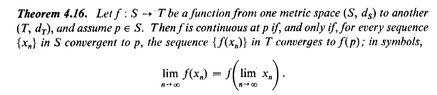Math Amateur
Gold Member
MHB
- 3,920
- 48
I am reading Tom M Apostol's book "Mathematical Analysis" (Second Edition) ...
I am focused on Chapter 4: Limits and Continuity ... ...
I need help in order to fully understand the example given after Theorem 4.29 ... ... Theorem 4.29 (including its proof) and the following example read as follows:
View attachment 9237
View attachment 9238
In the Example above we read the following:
" ... ... However, $$f^{ -1 }$$ is not continuous at the point $$f(0)$$. For example, if $$x_n = 1 - 1/n$$, the sequence $$\{ f(x_n) \}$$ converges to $$f(0)$$ but $$\{ x_n \}$$ does not converge in $$S$$. ... ... "My question is as follows:
Can someone please explain exactly how/why ... the sequence $$\{ f(x_n) \}$$ converges to $$f(0)$$ but $$\{ x_n \}$$ does not converge in $$S$$ ... ... implies that $$f^{ -1 }$$ is not continuous at the point $$f(0)$$ ... ... ?
-----------------------------------------------------------------------------------------------------------------------------------------------My thoughts ...
I think that the relevant theorem regarding answering my question is Apostol, Theorem 4.16 which reads as follows:View attachment 9239
If we let $$t_n \in f(S)$$ be such that $$t_n = f(x_n)$$ ... so the sequence $$\{ t_n \} = \{ f(x_n) \}$$ is in the domain of $$f^{ -1 }$$ ...
Then ... sequence $$\{ t_n \} = \[ f(x_n) \}$$ converges to $$f(0) = t_0$$ say ...
Then following Theorem 4.16 above ... for $$f^{ -1 }$$ to be continuous we need $$\{ f^{ -1 } (t_n) \} = \{ f^{ -1 } ( f(x_n) ) \} = \{ x_n \}$$ to converge in $$S$$ ... but it does not do so ...
(mind you ... I'm not sure how to prove it doesn't converge in $$S$$ ...)
Is that correct?
-------------------------------------------------------------------------------------------------------------------------------------------------------------------
Hope that someone can help ...
Peter
I am focused on Chapter 4: Limits and Continuity ... ...
I need help in order to fully understand the example given after Theorem 4.29 ... ... Theorem 4.29 (including its proof) and the following example read as follows:
View attachment 9237
View attachment 9238
In the Example above we read the following:
" ... ... However, $$f^{ -1 }$$ is not continuous at the point $$f(0)$$. For example, if $$x_n = 1 - 1/n$$, the sequence $$\{ f(x_n) \}$$ converges to $$f(0)$$ but $$\{ x_n \}$$ does not converge in $$S$$. ... ... "My question is as follows:
Can someone please explain exactly how/why ... the sequence $$\{ f(x_n) \}$$ converges to $$f(0)$$ but $$\{ x_n \}$$ does not converge in $$S$$ ... ... implies that $$f^{ -1 }$$ is not continuous at the point $$f(0)$$ ... ... ?
-----------------------------------------------------------------------------------------------------------------------------------------------My thoughts ...
I think that the relevant theorem regarding answering my question is Apostol, Theorem 4.16 which reads as follows:View attachment 9239
If we let $$t_n \in f(S)$$ be such that $$t_n = f(x_n)$$ ... so the sequence $$\{ t_n \} = \{ f(x_n) \}$$ is in the domain of $$f^{ -1 }$$ ...
Then ... sequence $$\{ t_n \} = \[ f(x_n) \}$$ converges to $$f(0) = t_0$$ say ...
Then following Theorem 4.16 above ... for $$f^{ -1 }$$ to be continuous we need $$\{ f^{ -1 } (t_n) \} = \{ f^{ -1 } ( f(x_n) ) \} = \{ x_n \}$$ to converge in $$S$$ ... but it does not do so ...
(mind you ... I'm not sure how to prove it doesn't converge in $$S$$ ...)
Is that correct?
-------------------------------------------------------------------------------------------------------------------------------------------------------------------
Hope that someone can help ...
Peter
Attachments
Last edited: