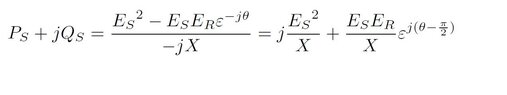How does theta transform into theta minus pi/2 in complex numbers?
- Context: MHB
- Thread starter aruwin
- Start date
Click For Summary
SUMMARY
The discussion centers on the transformation of the angle theta into theta minus pi/2 within the context of complex numbers, specifically using Euler's formula. Participants clarify that the equation ie^{-i\theta}=e^{i\left(\frac{\pi}{2}-\theta\right)} is valid by demonstrating the relationship through co-function identities and the properties of the imaginary unit i. The transformation is confirmed by showing that i = e^{i \frac{\pi}{2}}, which resolves the apparent discrepancy in the equation.
- Understanding of Euler's formula in complex analysis
- Familiarity with co-function identities for sine and cosine
- Knowledge of complex exponentials and their properties
- Basic algebraic manipulation of complex numbers
- Study the derivation and applications of Euler's formula in complex analysis
- Explore co-function identities and their implications in trigonometry
- Learn about the properties of the imaginary unit
iin complex numbers - Investigate the geometric interpretation of complex exponentials on the unit circle
Students and professionals in mathematics, physics, and engineering who are working with complex numbers and trigonometric identities, particularly those focusing on signal processing or wave mechanics.
Similar threads
High School
Is this a complex number at the second quadrant?
- · Replies 7 ·
- · Replies 2 ·
- · Replies 13 ·
- · Replies 12 ·
- · Replies 7 ·
High School
Getting from complex domain to real domain
- · Replies 3 ·
- · Replies 5 ·
- · Replies 2 ·
- · Replies 19 ·
- · Replies 2 ·