tomtomtom1
- 160
- 8
- Homework Statement
- I am now trying to understand how a uniformally distributed force and a non uniformally distributed force acts on a shape.
- Relevant Equations
- I am now trying to understand how a uniformally distributed force and a non uniformally distributed force acts on a shape.
Hello all
After a lot of support from people like [U]Dr.D[/U], [U]mfig[/U] and [U]collinsmark[/U] I have finally understood the concept of Centriods and Centre of Mass.
I am now trying to understand how a uniformally distributed force and a non uniformally distributed force acts on a shape.
If I had an oddly shaped object for which I found the centre of mass and its surface area.
I then applied a uniformly distributed force of 100N on that object's surface, then would I be correct in saying that the uniformly distributed force of 100N is converted to an equivalent point force by multiplying the area by the force. The equivalent point force then acts through the objects centre of mass.
Below is a picture of what I am trying to understand:-
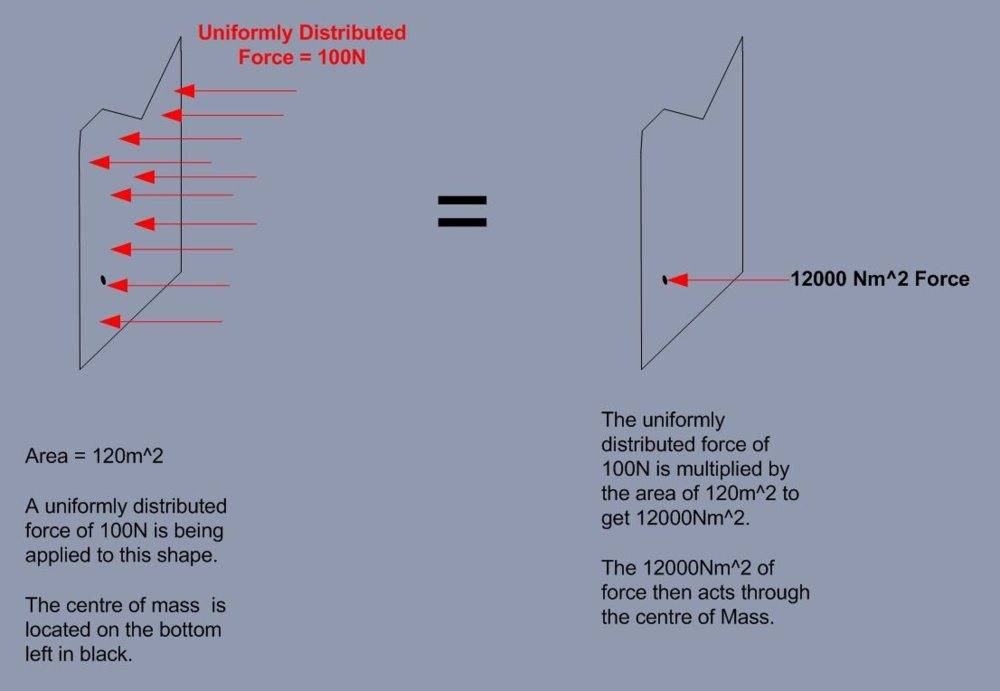
Would this illustration be correct?
Thank you.
After a lot of support from people like [U]Dr.D[/U], [U]mfig[/U] and [U]collinsmark[/U] I have finally understood the concept of Centriods and Centre of Mass.
I am now trying to understand how a uniformally distributed force and a non uniformally distributed force acts on a shape.
If I had an oddly shaped object for which I found the centre of mass and its surface area.
I then applied a uniformly distributed force of 100N on that object's surface, then would I be correct in saying that the uniformly distributed force of 100N is converted to an equivalent point force by multiplying the area by the force. The equivalent point force then acts through the objects centre of mass.
Below is a picture of what I am trying to understand:-
Would this illustration be correct?
Thank you.