How is an autocorrelation function computed? (Dynamic Light Scattering)

[Salmone]

In an experiment of Dynamic Light Scattering, how is an autocorrelation like the one in the image computed?

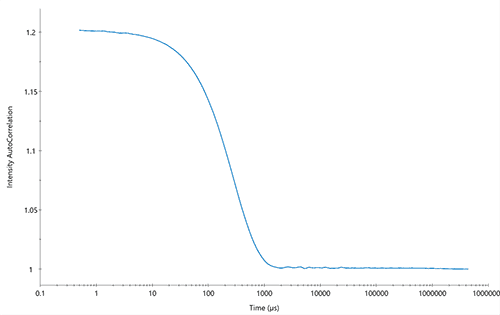
Mathematically a correlation function can be written as $G(\tau)=\langle I(t)I(t+\tau) \rangle$, in an experiment like the one I mentioned the scattered intensity light is collected by a single detector, then the signal is sent to a digital correlator which computes the correlation function. How this process works? Once I have a signal from the detector, what does the correlator do? Does it multiply the intensity at time $t$ with the same intensity at time $t+\tau$ simply? How is the average implemented? By recording with the detector the same scattered intensity multiple times? Can you explain very generally how a digital correlator works?

 

[Baluncore]

Can you explain very generally how a digital correlator works?

A correlator would take the FFT of the two signals, multiply those two spectra, then inverse FFT. In effect, filtering a signal by another signal.

I expect autocorrelation could be performed by taking the FFT of the signal, squaring the vectors of the resulting spectrum, then computing the inverse FFT. In effect, filtering a signal by itself.