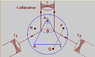
How is the Refracting Angle of a Prism Calculated Using θ and θ/2?

[Outrageous]

Homework Statement

Why the angle of a prism can be calculated by measuring θ , and then θ/2 ?

Homework Equations

The Attempt at a Solution

Really no idea about it , please guide .Thank you.

 

[Outrageous]

One more question , why the light ray from the collimator reflected not refracted?
Thank you.

 

[rude man]

Is the prism immersed in a spherical liquid of n > n of prism? Then you can get total internal reflection of the incoming beam back into the sphere.

 

[Outrageous]

No, the outside medium is air. I read and checked books but I can't find one to prove θ/2=refracting angle of prism. Please guide . Thank you.

 

[haruspex]

Not sure I understand the picture. It looks like a circular prism with a triangular hollow.

 

[rude man]

Not sure I understand the picture. It looks like a circular prism with a triangular hollow.

Which could account for total internal reflection back into the circular prism.

 

[Outrageous]

ABC is a transparent prism .
A is the refracting angle of a prism.
T is telescope to receive the reflected light.
This is an experiment to find A.
A lot of books did say this is an easy way to find A . But I can't find how . Please guide. Thank you.

 

[haruspex]

Ok, so this nothing to do with refraction. It's simply a geometry problem. The prism might as well be a pair of mirrors at angle A.
The incident light makes an angle A/2 to the surface, and is reflected at angle A/2 to the surface. Therefore each reflection is at angle A to its corresponding incident ray. Since the rays each side are turned through angle A in opposite directions, they now diverge at angle 2A = theta.

 

[Outrageous]

The incident light makes an angle A/2 to the surface, and is reflected at angle A/2 to the surface.

How do we make the incident light at an angle A/2 to the surface of mirror?

Therefore each reflection is at angle A to its corresponding incident ray. Since the rays each side are turned through angle A in opposite directions, they now diverge at angle 2A = theta.

How to know reflection is at angle A to its incident ray ? or do you mean the incident light makes an angle A/2 to the normal?

Thank you

 

[haruspex]

How do we make the incident light at an angle A/2 to the surface of mirror?

Simple geometry. Draw a line bisecting the angle A. It is parallel to the incident beam, so that line and the beam make the same angle to the surface.
However, it is important that it does not need to be exactly A/2. Suppose you set it up a little bit askew, so the beam makes an angle A/2+x to one surface, and therefore an angle A/2-x to the other.
A reflected beam makes the same angle to the surface as the incident beam, so these are also A/2+x, A/2-x respectively. One beam is therefore 'turned' through an angle of A+2x, the other through an angle of A-2x,. Adding these up still gives 2A as the divergence between them.

 

[Outrageous]

Totally understand already . Really thank you . No wonder physics books don't show, it is just a math problem. Thank you so much

 

[Outrageous]

http://www.pinkmonkey.com/studyguides/subjects/physics/chap16/p1616601.asp

Can you please explain to me why AQRS is a cyclic quadrilateral?
Thank you

 

[haruspex]

http://www.pinkmonkey.com/studyguides/subjects/physics/chap16/p1616601.asp

Can you please explain to me why AQRS is a cyclic quadrilateral?

It doesn't define the point R, but it looks like it is chosen as the point where the normals at Q and S intersect. So by definition the angles that AR subtends at Q and S are each right angles. That makes AQRS a cyclic quadrilateral, i.e. its vertices lie on a circle, and AR is a diameter of that circle.

 

[Outrageous]

But do we have enough to prove Q and S are lie on the circumference?
Use the centre of circle?

 

[haruspex]

But do we have enough to prove Q and S are lie on the circumference?
Use the centre of circle?

Yes. You can define a circle uniquely by declaring that AR is diameter. Any right-angled triangle you then draw with AR as hypotenuse will have its third vertex on the circumference of the circle. This is pretty basic geometry.

 

[Outrageous]

Yup, you are totally correct.
Thank you.