How many ways to sum vectors in a plane to zero

[bkraabel]

Homework Statement

(a) Suppose you have two arrows of equal length on a
tabletop. If you can move them to point in any direction
but they must remain on the tabletop, how many distinct
patterns are possible such that the arrows, treated as vectors,
sum to zero? [Note: If a pattern cannot be rotated on the
tabletop to match another pattern in your list, it is a distinct
pattern.] (b) Repeat part a for three arrows. (c) Repeat for
four arrows. (d) Do you recognize a relationship between
the number of arrows (vectors) and the number of distinct
patterns?

Homework Equations

Sums of x and y components are zero (gives two equations). Magnitudes are all the same (gives n - 1 equations, where n is the number of vectors).

The Attempt at a Solution

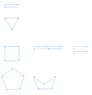
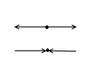
See attachment.
For two vectors, only solution is to have them point in opposite directions.
For three vectors, only solution I can think of is an equilateral triangle.
For four vectors, I can think of three solutions: square, two vectors pointing right and two pointing left, then one right, one left, one right, one left
For five vectors, I can find two solutions: pentagon, pentagon with one adjacent pair of vectors inverted.

 

[berkeman]

For the solutions that form closed figures, can you do something that will double the number of closed figures?

 

[barryj]

What about a star?

 

[CWatters]

For two vectors, only solution is to have them point in opposite directions.

There is more than one way to do that.

For three vectors, only solution I can think of is an equilateral triangle.

For four vectors, I can think of three solutions: square, two vectors pointing right and two pointing left, then one right, one left, one right, one left

Shapes like that don't work. There would be a net torque. Does that matter?

 

[bkraabel]

For two vectors, how many unique ways can you arrange two antiparallel equal-length vectors (i.e., ways that cannot be made equal by rotating the arrangement of vectors)?? Seems to me there is only one way to do it (see attached drawing). All other possibilities are just rotations of the first, no??

Regarding torque, it doesn't matter. This is purely a mathematical exercise, so we just need to have the vectors sum to zero.

thanks for the help!

 

[haruspex]

I feel the question intends you to treat these as pure vectors, i.e. place each arrow as pointing from the origin. (Or, equivalently, to consider any rearrangement consisting of a mere translation of arrows as the same arrangement. If not, there are infinitely many arrangements in every case.)
Consequently I agree there are unique solutions for 2 and 3 vectors. Beyond that, you're missing rather a lot.

 

[CWatters]

Yes it's not clear if the question counts this as one or two distinct patterns ...

 

[bkraabel]

From the context of the book, I think that "treated as vectors" implies that you add them by arranging your arrows on the table top tip to tail. So, in this scenario, neither of these two patterns would qualify since they're not tip to tail (although mathematically they're correct).

 

[CWatters]

With 4 vectors the answer appears infinite.

EDIT: Ah ok if they have to be head to tali that's different.

EDIT 1: No I still get an infinite number if there are four vectors.

 

[CWatters]

From the context of the book, I think that "treated as vectors" implies that you add them by arranging your arrows on the table top tip to tail. So, in this scenario, neither of these two patterns would qualify since they're not tip to tail (although mathematically they're correct).

Ah ok so like this..

 

[bkraabel]

I guess that's my question: what arrangements am I missing for four vectors?

Note that I tried my hand at five vectors just to see if that made it easier to spot a pattern -- it doesn't (at least for me).

Anyone care to take a stab at the relationship between the number of vectors and the number of unique arrangements of these vectors that sum to zero? I don't see it.

 

[CWatters]

I guess that's my question: what arrangements am I missing for four vectors?

A diamond shape, with variable angles.

 

[haruspex]

From the context of the book, I think that "treated as vectors" implies that you add them by arranging your arrows on the table top tip to tail. So, in this scenario, neither of these two patterns would qualify since they're not tip to tail (although mathematically they're correct).

Head-to-tail and star from origin are merely two representations. A given set of vectors has a unique representation as star-from-origin, but with three or more could have multiple representations as a polygon.

 

[consciousness]

For four there are infinite rhombuses that can be formed.