How much does the raft move with change of position?

[ninesixfive]

heres the problem...

and i figured out part a but don't understand how to get the second part, here is what i have done...

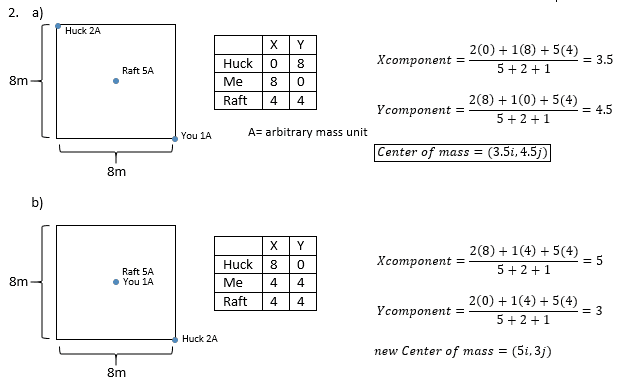
my question is should the angle be from the point of origin? what I am getting is -2.12 meters in a direction of -45 degrees. is this correct? I'm using x2-x1/y2-y1 to get 1.5/-1.5 then using Pythagorean to get the distance of shift and using arctan(-1.5/1.5) to get the -45 ?

 

[mfb]

my question is should the angle be from the point of origin?

The vector does not need a reference point, just a reference direction. Relative to the x-axis should be fine. Or relative to some other direction which you clearly describe. Like "from the center towards the new position of [...]".
The magnitude should be positive.

 

[ninesixfive]

So could I say the raft moves 2.12 meters in a direction of 135 degrees when viewing form above?

 

[mfb]

If you clarify 135 degrees relative to what, sure.

 

[ninesixfive]

relative to the point of origin (bottom left corner)... looking at it from above it would move into the the third quadrant , of course the raft would stay square to the x and y axis