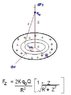
The discussion focuses on applying the Binomial Theorem to solve equations involving surface charge density (dq), surface area (da), and point charges (qo) in relation to a ring's geometry. Specifically, it addresses scenarios where the distance from the center of the ring to the point charge (Z) is either zero or significantly greater than zero (Z >> 0). The participants suggest that this topic is best suited for physics forums or homework sections, indicating a need for specialized knowledge in physics to tackle the problem effectively.
PREREQUISITESStudents and professionals in physics, particularly those studying electrostatics and mathematical applications in physical scenarios. This discussion is beneficial for anyone looking to deepen their understanding of the Binomial Theorem in relation to electric charge distributions.
