NicolaiTheDane
- 100
- 10
First let me preface this by saying, I'm not a native english speaker. I'm not sure "uncertainty" is the word I'm looking for it might also be deviation, however it is the translation of what its called in Danish, my native tongue.
I'm doing a lab report about rolling objects on a slope, for my classic in classical mechanics at the Niels Bohr Institute. We have been told to assign and calculate appropriate "uncertainty" to our results, both experimental and theoretical. We are very sure we doing it right for either.
1. Homework Statement
We don't know how to calculate the uncertainty/deviation of our values for "I" the moment of inertia.
Most importantly though, we don't know what to do, when we have both statistical uncertainty/deviation, as well as instrumental uncertainty/deviation/accuracy.
The equation we have been told to use, for our theoretical uncertainty:
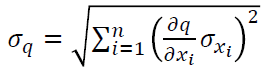
The equation we are using for the moment of inertia:
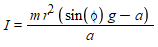
I = Moment of Inertia, m = mass of the rolling object, r = radius of the object, g = gravitation acceleration, a = tangential acceleration of the rolling object.
To keep things simple, we did the following to get an uncertainty of our measured moment of inertia for one of the objects:
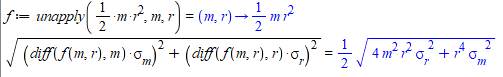
Where sigma_m is the accuracy of the weight, and the sigma_r is the accuracy of my caliper. Now we aren't sure this is correct, so it would be nice to have it confirmed or denied.
The second and more involved problem, is that of our experimental moment of inertia. Our experiment yields a tangential acceleration, which we use in our equation for "I", which is mentioned further up, to find the moment of inertia.
The experiment is a slope, with 5 photocell detectors wired in a series, and plugged into an oscilloscope. We calculate the acceleration as follows:
v = Δx/Δt, a = 2*(v2-v1)/t3-t1
Where Δx between each photocell is measured using the caliper. This gives us 3 average accelerations pr run of the experiment, giving us an overall average acceleration pr run of a = (a1+a2+a3)/3 and a statistical deviation sigma = std([a1,a2,a3])/sqrt(3) (We use matlab; std() returns the standard deviation between elements of a vector)
Now this is where we the problem comes. We are running the experiment several times pr object, in order to minimize the statistical deviation. What we are doing is after finding the overall average acceleration and sigma pr experiment, we then do the same to them, to get an overall acceleration and sigma for the object.
Given that we have no statistical knowledge, and thus have no clue about how or why the sigma thing is treated the way it is, we don't know if this is the right way to handle it. Nor do we know how to apply the uncertainty of the caliper, which is used to measure Δx, to our resulting acceleration.
I'm not sure I have described the problem accurately enough, so if its just a mess, let me know, and I'll try to clarify. Thanks in advance for any and all aid.
I'm doing a lab report about rolling objects on a slope, for my classic in classical mechanics at the Niels Bohr Institute. We have been told to assign and calculate appropriate "uncertainty" to our results, both experimental and theoretical. We are very sure we doing it right for either.
1. Homework Statement
We don't know how to calculate the uncertainty/deviation of our values for "I" the moment of inertia.
Most importantly though, we don't know what to do, when we have both statistical uncertainty/deviation, as well as instrumental uncertainty/deviation/accuracy.
Homework Equations
The equation we have been told to use, for our theoretical uncertainty:
The equation we are using for the moment of inertia:
I = Moment of Inertia, m = mass of the rolling object, r = radius of the object, g = gravitation acceleration, a = tangential acceleration of the rolling object.
The Attempt at a Solution
To keep things simple, we did the following to get an uncertainty of our measured moment of inertia for one of the objects:
Where sigma_m is the accuracy of the weight, and the sigma_r is the accuracy of my caliper. Now we aren't sure this is correct, so it would be nice to have it confirmed or denied.
The second and more involved problem, is that of our experimental moment of inertia. Our experiment yields a tangential acceleration, which we use in our equation for "I", which is mentioned further up, to find the moment of inertia.
The experiment is a slope, with 5 photocell detectors wired in a series, and plugged into an oscilloscope. We calculate the acceleration as follows:
v = Δx/Δt, a = 2*(v2-v1)/t3-t1
Where Δx between each photocell is measured using the caliper. This gives us 3 average accelerations pr run of the experiment, giving us an overall average acceleration pr run of a = (a1+a2+a3)/3 and a statistical deviation sigma = std([a1,a2,a3])/sqrt(3) (We use matlab; std() returns the standard deviation between elements of a vector)
Now this is where we the problem comes. We are running the experiment several times pr object, in order to minimize the statistical deviation. What we are doing is after finding the overall average acceleration and sigma pr experiment, we then do the same to them, to get an overall acceleration and sigma for the object.
Given that we have no statistical knowledge, and thus have no clue about how or why the sigma thing is treated the way it is, we don't know if this is the right way to handle it. Nor do we know how to apply the uncertainty of the caliper, which is used to measure Δx, to our resulting acceleration.
I'm not sure I have described the problem accurately enough, so if its just a mess, let me know, and I'll try to clarify. Thanks in advance for any and all aid.
Attachments
-
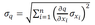 upload_2017-12-16_14-0-51.png2.9 KB · Views: 519
upload_2017-12-16_14-0-51.png2.9 KB · Views: 519 -
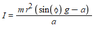 upload_2017-12-16_14-2-32.png911 bytes · Views: 531
upload_2017-12-16_14-2-32.png911 bytes · Views: 531 -
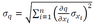 upload_2017-12-16_14-8-38.png2.2 KB · Views: 697
upload_2017-12-16_14-8-38.png2.2 KB · Views: 697 -
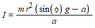 upload_2017-12-16_14-8-58.png925 bytes · Views: 515
upload_2017-12-16_14-8-58.png925 bytes · Views: 515 -
 upload_2017-12-16_14-10-56.png2.5 KB · Views: 508
upload_2017-12-16_14-10-56.png2.5 KB · Views: 508 -
 upload_2017-12-16_14-12-44.png6.5 KB · Views: 526
upload_2017-12-16_14-12-44.png6.5 KB · Views: 526 -
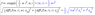 upload_2017-12-16_14-21-36.png3.2 KB · Views: 696
upload_2017-12-16_14-21-36.png3.2 KB · Views: 696