How to Calculate Bolt Reaction Forces Under Different Loading Conditions?

[enotyphoon]

*Note: Even for 1 answer for any of the question, I am highly appreciate it. I am understand it quite a burden to answer all. Thank you.

Hi guys,

I am currently seeking a correct approach of getting the reaction force developed on bolt due to the Forward or Upward force experience by the object as per regulation of Title 14 CFR 27.561.

Imagine I have a box secure on plate by 4 bolts in symmetrical way. The box will experience forward force of 20 forward or 4g upward. Hence I have to select the bolt that can withstand these condition. Initially for both cases, I would simply divided the force by 4 to find the reaction on bolt with assumption the C.G of box is located at nicely at the middle between 4 bolt (symmetrical).

Since I would like to know the proper way of finding this reaction force, I have develop a FBD for this case as below.

Basic:

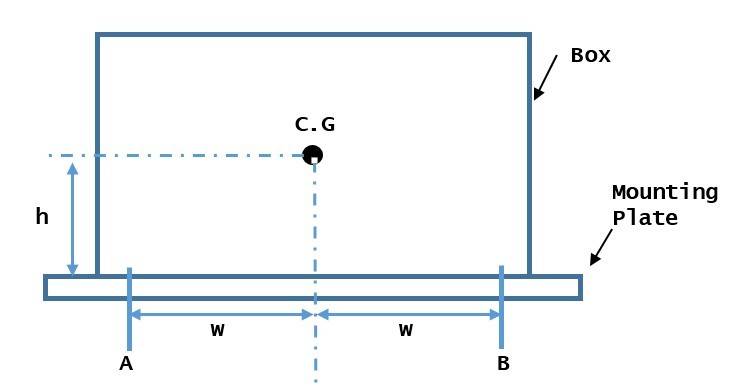
Box experiencing upward force case;

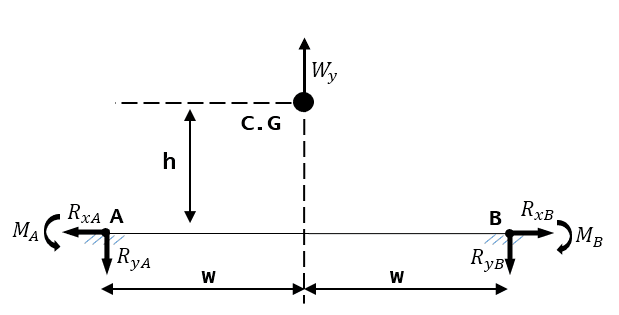
Box experiencing forward force case;

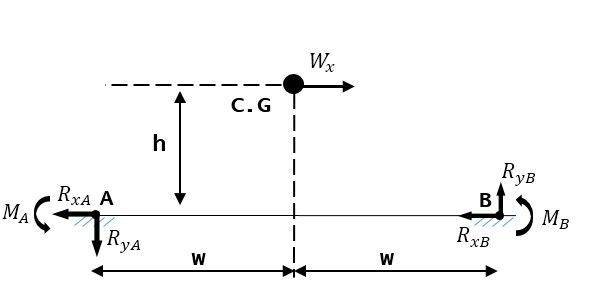
*A and B are Bolted connection, so I am using fixed support. However still not sure if it the correct presentation anc correct support. Correct me if I'm wrong in presenting it.
*Neglecting the effect c.g of plate as it thickness is negligible.

My main concern to find is only on the reaction forces and my question are:
1) Does my basic understanding in this case is correct based on the FBD above?

Upward Force case:-
2) Does it simply divided by 2 to find Rxa or Rxb(due to symmetrical)?, and divided again by 2 to find force on each bolt (4 bolt in symmetrical position, 2 front:2 back)
3) Does height of C.G have effect on finding value of Rxa?
4)I might encounter case where the c.g is not symmetrical with bolt. it is applicable using this equation for this case(diagram below). Since I'm not sure weather it is compatible with my FBD or not.

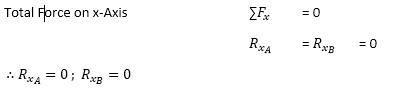
5) is this equation valid for upward case above? and if upward force is not in symmetry between the bolts, does Rx still zero?

Forward Force case;
5) to find Rxa, I would simply divide by 2 as per Figure below and divide by 2 again to gain force in each bolt (not shown in figure). Is this correct?

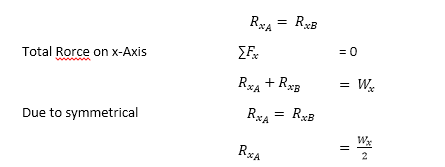
6) If the c.g is not located at the middle between Fxa and Fxb, does equation as figure above applies? (in other word, does location of c.g have effect on shear stress?)
7) If there is more bolts like 3 pairs at the back and 3 pairs at front (Fxa & Fxb have pair of bolt, Figure below). Does shear force (Fx) is same for all pairs of bolt regardless its position.

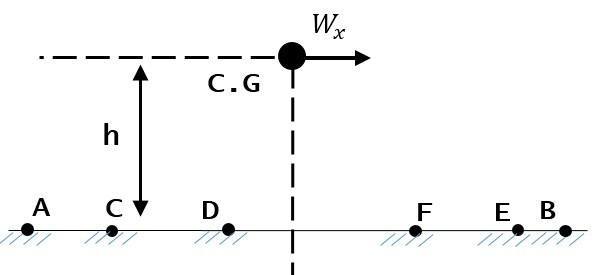
Sorry for asking very much question, just need to clarify. Feel free to answer any question. Would be glad if you all could help me although with one answer. Do not hesitate to share your opinion.

Thank you.

 

[PhanthomJay]

The bolts should be treated as pinned supports. They can take axial and shear loads but not moments. For the upward symmetrical 4 bolt case, each bolt supports one quarter of the upward load in tension and each has no shear. If the load is not applied at center, you should solve tensile reaction forces accordingly as a pinned pinned beam. For the transverse load case, Bolts take shear and tension. Shear divided equally. Tension determine by simple beam subject to a couple. For multiple bolts with the transverse load, you need to find the moment of inertia of bolt pattern and use Mr/I for bolt load calcs (outer bolts will see more load)

 

[enotyphoon]

The bolts should be treated as pinned supports. They can take axial and shear loads but not moments. For the upward symmetrical 4 bolt case, each bolt supports one quarter of the upward load in tension and each has no shear. If the load is not applied at center, you should solve tensile reaction forces accordingly as a pinned pinned beam. For the transverse load case, Bolts take shear and tension. Shear divided equally. Tension determine by simple beam subject to a couple. For multiple bolts with the transverse load, you need to find the moment of inertia of bolt pattern and use Mr/I for bolt load calcs (outer bolts will see more load)

However sir, the bolt is preventing the beam from being turn. Don't it should have moment?. If it is pin-pin, it mean the beam can travel in rotation at the end hence it has no moment while the bolt prevent it.
Could you explain detail sir on this confusion pin - pin or fix-fix for bolted connnection? I'm highly appreciated.

For multiple transverse load. The shear force for each bolt is divided equally from main forward force regardless it distamce from c.g isn't??

Thank you sir.

 

[256bits]

If it is pin-pin, it mean the beam can travel in rotation at the end hence it has no moment while the bolt prevent it.

Sure. The bolts cannot withstand a torque, only shear or axial load.
That does not mean there will not be a moment to contend with at location A or B.

 

[enotyphoon]

Sure. The bolts cannot withstand a torque, only shear or axial load.
That does not mean there will not be a moment to contend with at location A or B.

are you saying at point A or B have a moment? seems to led to a fix-fix support.

 

[256bits]

are you saying at point A or B have a moment? seems to led to a fix-fix support.

The structure itself can have a moment applied to it.
How does the moment applied to the structure translate into forces at the supports.

Take a rod with a hinge, or pinned, support at one end.
Forces applied to the rod, will result in the pin supporting forces only be in the x and y direction.
Any moment on the rod, as a result of the forces or torques applied to the rod, will cause the rod to rotate.

For no rotation, the other end of the rod can be supported by another pin support.

 

[PhanthomJay]

For multiple transverse load. The shear force for each bolt is divided equally from main forward force regardless it distamce from c.g isn't??

Thank you sir.

due to the rigidity of the system under transverse shear at the connections, it is (my) common practice to assume that all bolts equally share the transverse shear load regardless of its point of application.