Brad_
- 6
- 0
Hi,
View attachment 1815
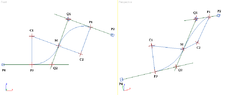
Given 3D points P1(200,60,140), P2(300,120,110), P3(3,0,-1), P4(-100,0,-1) and the radius of
arc C1MP3 is equal to radius of arc C2MP1. How do I calculate coordinates x, y, z of
points C1 and C2?
Points C1 and C2 are centers of two reverse arcs which are tangent to each other at point M which lies on ray Q1Q2.
Arc C1MP3 is tangent to ray P3P4 and arc C2MP1 is tangent to ray P1P2.
Points Q1 and Q2 emerge as a result of moving points P1 and P3 in the direction obvious from picture.
It is easy to calculate centers of arcs with different radius. But how to calculate centers of arcs
with equal radius. How to find the position of points Q1 and Q2?
View attachment 1815
Given 3D points P1(200,60,140), P2(300,120,110), P3(3,0,-1), P4(-100,0,-1) and the radius of
arc C1MP3 is equal to radius of arc C2MP1. How do I calculate coordinates x, y, z of
points C1 and C2?
Points C1 and C2 are centers of two reverse arcs which are tangent to each other at point M which lies on ray Q1Q2.
Arc C1MP3 is tangent to ray P3P4 and arc C2MP1 is tangent to ray P1P2.
Points Q1 and Q2 emerge as a result of moving points P1 and P3 in the direction obvious from picture.
It is easy to calculate centers of arcs with different radius. But how to calculate centers of arcs
with equal radius. How to find the position of points Q1 and Q2?