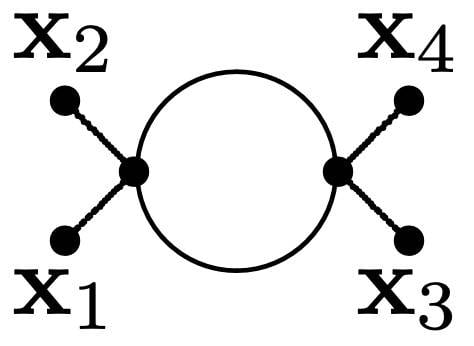
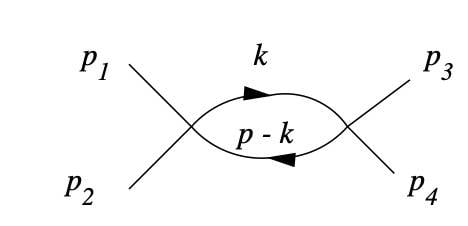
SUMMARY
This discussion focuses on calculating the Feynman amplitude for a specific Fish diagram, particularly in the context of quantum field theory (QFT). The user seeks step-by-step study materials for understanding this process, emphasizing cases where particles x_3 and x_4 can be scalar, fermion, or gauge boson. Recommended resources include QFT texts such as "Quantum Field Theory in a Nutshell" by Srednicki and "An Introduction to Quantum Field Theory" by Peskin & Schroeder, specifically referencing Section 5.4.3 for simple ##\phi^4## theory.
PREREQUISITES
- Understanding of tree-level Feynman diagrams
- Familiarity with quantum field theory (QFT) concepts
- Knowledge of scalar, fermion, and gauge boson particles
- Basic proficiency in mathematical techniques used in QFT
NEXT STEPS
- Study "Quantum Field Theory in a Nutshell" by Srednicki for foundational concepts
- Explore "An Introduction to Quantum Field Theory" by Peskin & Schroeder for detailed calculations
- Review Section 5.4.3 of the provided lecture notes on ##\phi^4## theory
- Practice calculating Feynman amplitudes for various particle interactions
USEFUL FOR
This discussion is beneficial for physics students, researchers in quantum field theory, and anyone interested in advanced particle physics calculations.