SUMMARY
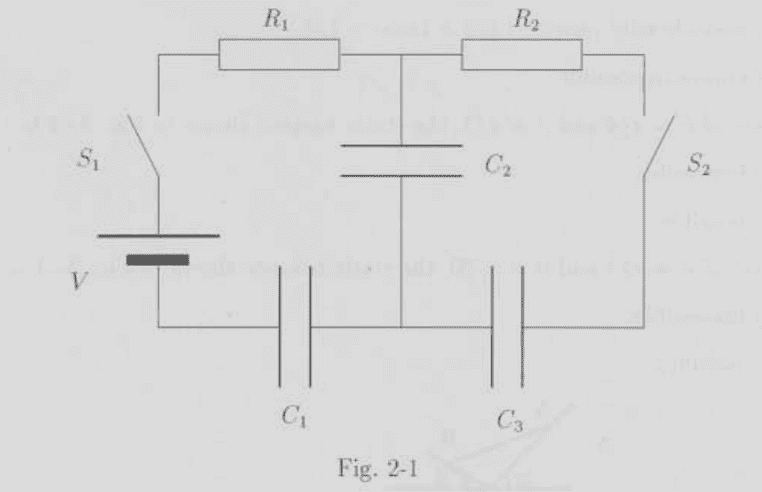
The discussion focuses on calculating the heat generated on resistor R2 after determining the voltage and charge in a circuit involving capacitors C1, C2, and C3. The voltage values identified are 4V and 2V, with a total charge of 8 Coulombs. Participants emphasize the importance of applying conservation of charge and voltage equality principles to derive the final charges on capacitors C2 and C3 after closing switch S2. The final charges are calculated as Q2 = 16/3 C and Q3 = 8/3 C, leading to the subsequent calculation of heat generated on resistor R2.
PREREQUISITES
- Understanding of capacitor charging and discharging processes
- Familiarity with Kirchhoff's Voltage Law (KVL)
- Knowledge of conservation of charge principles
- Basic electrical units: Volts, Coulombs, and Farads
NEXT STEPS
- Learn how to apply Kirchhoff's Voltage Law in capacitor circuits
- Study the principles of charge conservation in electrical circuits
- Explore methods for calculating heat generated in resistors using Joule's law
- Investigate the behavior of capacitors in series and parallel configurations
USEFUL FOR
Electrical engineering students, circuit designers, and anyone involved in analyzing capacitor circuits and heat generation in resistors.