kau
- 53
- 0
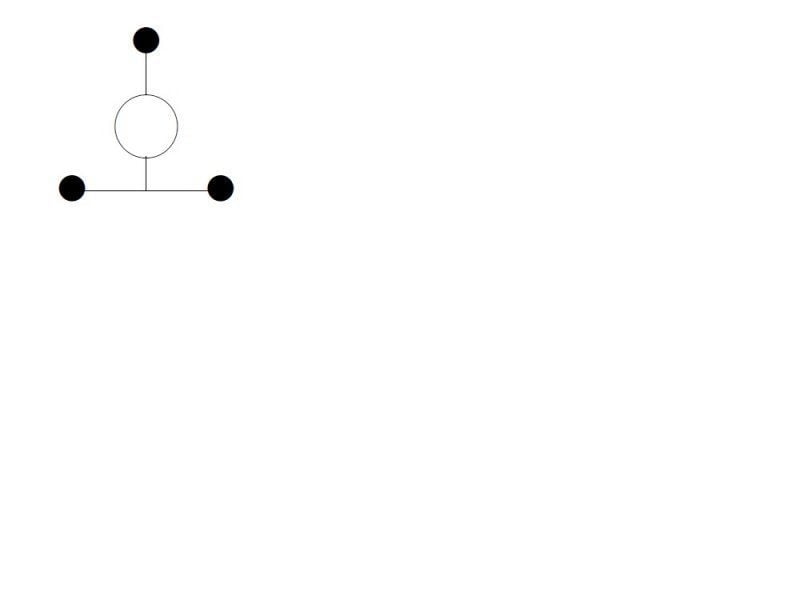
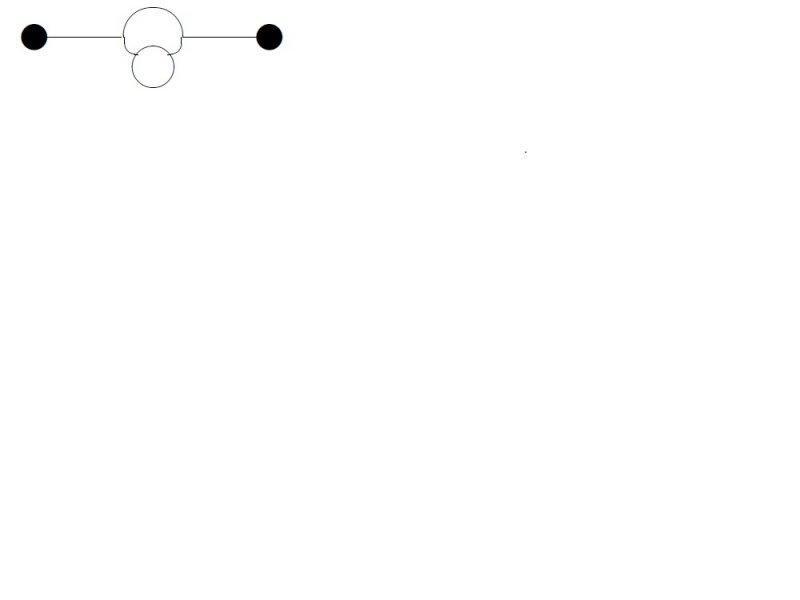
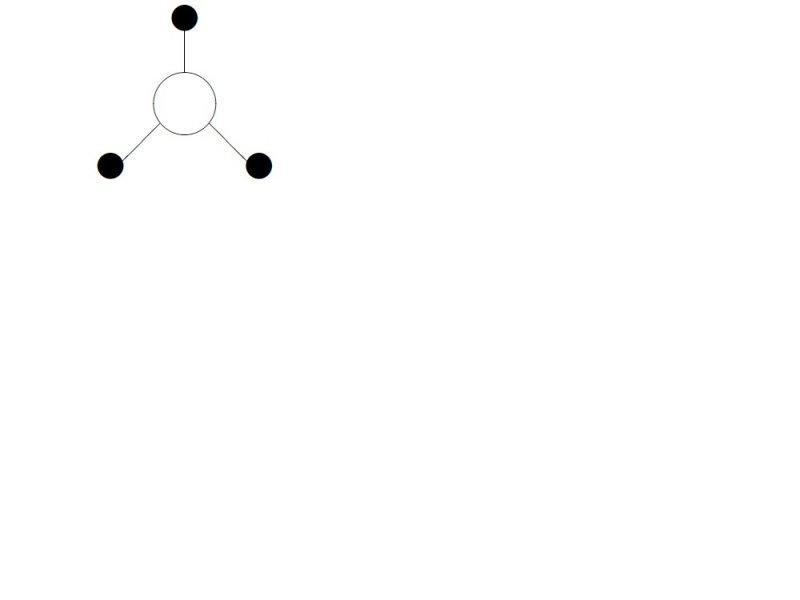
I am reading Srednicki's book and I am stuck at this point of calculating symmetry factors for Feynman's Graph in the context of dealing with interacting scalar field. First of all my question is what is the standard procedure to calculate it. The way Srednicki has talked about it is that if interchanging any two things match with any other swapping then we should take into account factor 2 for each of that case. First of all I didn't understand what does it mean to interchange two legs of vertices. which part is called leg of a vertex? alright then consider the four diagrams I have attached below. And explain me the factors in each case using the kind of arguments like swapping this and that and so on. then answer these ques.. In the first diagram can I swap all three sources?? in the third diagram can I swap the lower two parts of the big bubble which is holding the lower loop?? Please help me. thanks.