babbagee
- 71
- 0
Hello
The question is
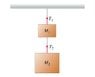
The blocks are now accelerating upward (due to the tension in the strings) with acceleration of magnitude a.
Find T2, the tension in the lower rope.
I really don't know where to start with this one. Would T2 equal the force that is applied on block one plus the weight that is pulling down. Point me in the right direction please.
Thanks
The question is
The blocks are now accelerating upward (due to the tension in the strings) with acceleration of magnitude a.
Find T2, the tension in the lower rope.
I really don't know where to start with this one. Would T2 equal the force that is applied on block one plus the weight that is pulling down. Point me in the right direction please.
Thanks
Attachments
Last edited: