Petrus
- 702
- 0
Calculate the length of the curve
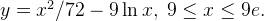
We got the formula $$\int_a^b\sqrt{1+[f'(x)]^2}$$
and $$f'(x)=\frac{x}{36}-\frac{9}{x} <=> \frac{x^2-324}{36x}$$
so now we got $$\int_9^{9e}\sqrt{1+(\frac{x^2-324}{36x})^2}$$
we can rewrite that as $$\int_9^{9e}\sqrt{1+\frac{(x^2-324)^2}{1296x^2}}$$
then do integration by part on it well I simply rewrite the function more too $$\int_9^{9e}\sqrt{\frac{1298x^2+(x^2-324)^2}{1296x^2}}$$ and set $$u=1298x^2+(x^2-324)^2$$ so we got $$dv=1296x^{-2}$$ so our $$du=2592x+2x^2-648+x$$ and $$v=\frac{1296x^{-3}}{-3}$$Is this correct?
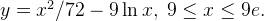
We got the formula $$\int_a^b\sqrt{1+[f'(x)]^2}$$
and $$f'(x)=\frac{x}{36}-\frac{9}{x} <=> \frac{x^2-324}{36x}$$
so now we got $$\int_9^{9e}\sqrt{1+(\frac{x^2-324}{36x})^2}$$
we can rewrite that as $$\int_9^{9e}\sqrt{1+\frac{(x^2-324)^2}{1296x^2}}$$
then do integration by part on it well I simply rewrite the function more too $$\int_9^{9e}\sqrt{\frac{1298x^2+(x^2-324)^2}{1296x^2}}$$ and set $$u=1298x^2+(x^2-324)^2$$ so we got $$dv=1296x^{-2}$$ so our $$du=2592x+2x^2-648+x$$ and $$v=\frac{1296x^{-3}}{-3}$$Is this correct?