MMS
- 146
- 4
Hi guys,
There are many calculators and applications out there that can calculate you the distance between Earth and Mars at every time, but I'm trying to find the actual function that gives me so and draw the path of it.
My objective is finding the distance R (and Phi of t), as shown below, as a function of time.
I'm trying to sort out some geometry here but I keep getting functions that are implicit (with R and Phi).
Any ideas how to find R and Phi and as a function of time each explicitly?
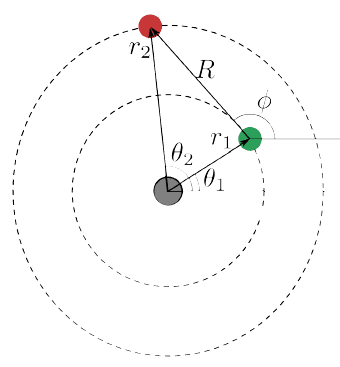
There are many calculators and applications out there that can calculate you the distance between Earth and Mars at every time, but I'm trying to find the actual function that gives me so and draw the path of it.
My objective is finding the distance R (and Phi of t), as shown below, as a function of time.
I'm trying to sort out some geometry here but I keep getting functions that are implicit (with R and Phi).
Any ideas how to find R and Phi and as a function of time each explicitly?