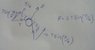Finding the magnitude of the force

[Muthumanimaran]

Homework Statement

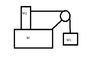
A force F is applied on the bigger mass 'M', which results in the prevention of smaller masses M1 and M2 moving with respect to larger mass M. The mass 'M' slides smoothly on the frictionless surface. Find the magnitude of the force. The pulley is ideal also consider the reaction force of pulley onto mass 'M'.

Homework Equations

The Attempt at a Solution

The normal force on the pulley is
$$R=2T \sin(\frac{\pi}{4})$$
The force on the system is
$$F=F_{1}+F_{2}+F_{3}$$
F1, F2, F3 are the forces on the masses M, M1 and M2 respectively.

The force F1
$$F_{1}=Ma-R\cos(\frac{\pi}{4})$$
$$F_{2}=M_{1}a$$
$$F_{3}=M_{2}a$$

If the masses M1 and M2 are at rest
$$T=M_{1}g$$
$$M_{2}a=M_{1}g$$

The force on the system is

$$F=(M+M_{1}+M_{2})\frac{M_{1}}{M_{2}}g-2M_{1}g\sin(\frac{\pi}{4})\cos(\frac{\pi}{4})$$
or
$$F=(M+M_{1})\frac{M_{1}}{M_{2}}g$$

I don't know whether my solution is correct. If I made an error, please give me a hint.

 

[kuruman]

It looks like you are guessing the magnitudes of forces instead of drawing free body diagrams for each mass. For example, why is this $R=2T \sin(\frac{\pi}{4})$ true?
If the three masses move together as one, then you should start by finding their common acceleration. Then draw FBDs for the masses. Also, do you think that mass M₁ is hanging vertically down as it accelerates to the right? What force (or component thereof) would provide the horizontal acceleration?

 

[Muthumanimaran]

It looks like you are guessing the magnitudes of forces instead of drawing free body diagrams for each mass. For example, why is this $R=2T \sin(\frac{\pi}{4})$ true?
If the three masses move together as one, then you should start by finding their common acceleration. Then draw FBDs for the masses. Also, do you think that mass M₁ is hanging vertically down as it accelerates to the right? What force (or component thereof) would provide the horizontal acceleration?

 

[kuruman]

There is nothing in the original drawing that says the angle is π/4, but OK we will set that aside. What about the other issues I raised in my previous post? Did you draw the FBDs?