How to Calculate the Pseudoinverse Using the SVD?

[nao113]

Homework Statement

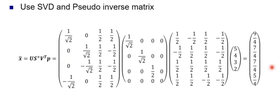
Hello, I have question related to SVD. Can anyone give me hints about what should I do to solve this question. I provided the question and my answer on the picture below. I have found the eigenvalues and eigenvector but I m not sure whether it is correct not and then whether this answer already cover the question. Thank you

Relevant Equations

𝐀=𝐔Σ𝐕∗

My Answer:
I am still beginner in this area so it s quite hard for me to understand this one. I am not sure what the output that this question asked me. I thought it might be asked about the value of x1, x2, x3, and x4

 

[SammyS]

Recheck that determinant for $~\mathbf{H^T H - I} \it \lambda$ .

 

[nao113]

Recheck that determinant for $~\mathbf{H^T H - I} \it \lambda$ .

Hello, thank you the respond, actually, I have correct my mistakes here. I already got the answer from this. But still, can you help me to understand what is U means? and how to get the matrix for it as well as Vt?

 

[Mark44]

But still, can you help me to understand what is U means?

U is a unitary matrix. See https://en.wikipedia.org/wiki/Unitary_matrix.

If U is a complex square matrix, it is unitary if its complex transpose (U*) is also its inverse. I.e., U* U = U U* = I.

 

[The Electrician]

Hello, thank you the respond, actually, I have correct my mistakes here. I already got the answer from this. But still, can you help me to understand what is U means? and how to get the matrix for it as well as Vt?

U is one of the parts of the SVD, which is given by U Σ V^T.
See: https://en.wikipedia.org/wiki/Singular_value_decomposition
Sometimes the letter S is used in place of Σ, which is the case in the image you've linked to.

The image you linked is trying to show how to calculate the pseudoinverse using the SVD: https://en.wikipedia.org/wiki/Moore–Penrose_inverse. See the heading about 2/3 of the way down the page: "Singular value decomposition (SVD)"

but they have made a mistake. They show the pseudoinverse as: US⁺V^T, but it should be VS⁺U^T

The numeric values they show are correct.

 

[nao113]

U is one of the parts of the SVD, which is given by U Σ V^T.
See: https://en.wikipedia.org/wiki/Singular_value_decomposition
Sometimes the letter S is used in place of Σ, which is the case in the image you've linked to.

The image you linked is trying to show how to calculate the pseudoinverse using the SVD: https://en.wikipedia.org/wiki/Moore–Penrose_inverse. See the heading about 2/3 of the way down the page: "Singular value decomposition (SVD)"

but they have made a mistake. They show the pseudoinverse as: US⁺V^T, but it should be VS⁺U^T

The numeric values they show are correct.

do you know how to change S to S+?

 

[The Electrician]

do you know how to change S to S+?

Re-read the section I linked to:

The image you linked is trying to show how to calculate the pseudoinverse using the SVD: https://en.wikipedia.org/wiki/Moore–Penrose_inverse. See the heading about 2/3 of the way down the page: "Singular value decomposition (SVD)"

"For a rectangular diagonal matrix such as S, we get the pseudoinverse by taking the reciprocal of each non-zero element on the diagonal, leaving the zeros in place, and then transposing the matrix. In numerical computation, only elements larger than some small tolerance are taken to be nonzero, and the others are replaced by zeros." Any of the elements that are very small (comparable to to the value of epsilon in the arithmetic of the math system you're using) are replaced by zero, not reciprocated."