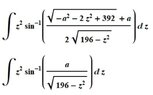How to calculate this type of integral, Thanks
Click For Summary
The discussion focuses on the calculation of two specific integrals involving the arcsine function and square roots. The first integral, $$\int {z}^{2}\arcsin\left({\frac{a+\sqrt{392-{a}^{2}-2{z}^{2}}}{2 \sqrt{196-{z}^{2}}}}\right) dz$$, is deemed unsolvable using the Wolfram Dev Platform. The second integral, $$\int {z}^{2}\arcsin\left({\frac{a}{\sqrt{196-{z}^{2}}}}\right) dz$$, is manageable but yields a complex and messy result. The Wolfram Language code provided for the second integral is: FullSimplify[Integrate[z^2 ArcSin[a/(Sqrt[196-z^2])],z] ]//TeXForm, which produces a lengthy expression involving logarithmic and inverse tangent functions.
- Understanding of integral calculus, particularly indefinite integrals
- Familiarity with the arcsine function and its properties
- Knowledge of complex numbers and logarithmic functions
- Experience with Wolfram Language and its syntax for integration
- Explore advanced techniques for solving complex integrals in Wolfram Language
- Study the properties and applications of the arcsine function in calculus
- Learn about the implications of complex logarithms in mathematical analysis
- Investigate numerical methods for approximating integrals that are difficult to solve analytically
Mathematicians, students studying calculus, and anyone interested in advanced integral computation and analysis using Wolfram Language.
Similar threads
- · Replies 4 ·
- · Replies 3 ·
- · Replies 6 ·
- · Replies 6 ·
- · Replies 9 ·
- · Replies 2 ·
- · Replies 3 ·
- · Replies 8 ·
- · Replies 12 ·