How to Combine Vector Directions for Animated Surfaces in OpenGL?

[ADDA]

Hi,

I have a question regarding vectors. I am thinking ahead regarding an application that I am writing in OpenGL. Currently, four functions make up the vertex calculations, with one independent variable (w2center, w2normal, w2uv, uv2vector). A per-vertex center variable and per-vertex vector basis, calculated from w2normal, gives additional input uv2vector or the function which outputs the vertex. I would like to be able to animate surfaces rendered by adding two functions t2center and t2normal. Vector translation should be simple for t2center with an addition operation of w2center, yet I am unable to think or remember which operation I would use to combine normals, or directions of the surface, with the two two functions w2normal and t2normal. Would someone suggest an operation?

Below is an example image. The process involves relative centering with a surface hierarchy. Axii are drawn from surface centers, red is x or i, green is y or j, blue is z or k. The sphere has a single point center, yet the second surface has a parabolic line as its center, which is slightly able to be viewed by the black dots below the x or i axis. Taking for normal the first derivative of the parabola, I would like to be able to move center through another function, t2center, which would then change the "normal" or direction of the per-vertex basis. I think that addition is correct for centers, yet which operation would I use to combine the normals?

 

[Mark44]

I have a question regarding vectors. I am thinking ahead regarding an application that I am writing in OpenGL. Currently, four functions make up the vertex calculations, with one independent variable (w2center, w2normal, w2uv, uv2vector). A per-vertex center variable and per-vertex vector basis, calculated from w2normal, gives additional input uv2vector or the function which outputs the vertex. I would like to be able to animate surfaces rendered by adding two functions t2center and t2normal.

Do you mean by writing these two functions or are you actually referring to some addtion operation?

Vector translation should be simple for t2center with an addition operation of w2center
, yet I am unable to think or remember which operation I would use to combine normals, or directions of the surface

What do you mean by "combine normals"?

, with the two two functions w2normal and t2normal. Would someone suggest an operation?

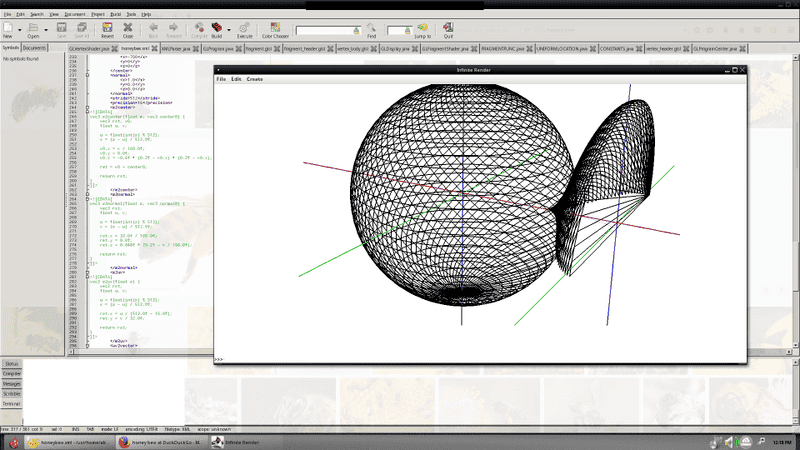
Below is an example image. The process involves relative centering with a surface hierarchy. Axii are drawn from surface centers, red is x or i, green is y or j, blue is z or k. The sphere has a single point center, yet the second surface has a parabolic line as its center, which is slightly able to be viewed by the black dots below the x or i axis. Taking for normal the first derivative of the parabola, I would like to be able to move center through another function, t2center, which would then change the "normal" or direction of the per-vertex basis. I think that addition is correct for centers, yet which operation would I use to combine the normals?

I am not understanding what you're trying to do here.

BTW, the plural of "axis" is "axes," not "axii."

 

[ADDA]

Thank you for your reply, Mark44. I am planning on using vector translation (addition) for dynamically changing the center point or curves, given a time variable, t.

With my current setup, the normal (or direction or first derivative of the center curve) would not combine with translation, rotation, an inner product or cross product. I'm defining the normal as a direction pointing in the positive x direction, the right as a direction pointing in the positive y direction, and the up as a direction pointing in the positive z direction. These three directions are what I refer to as a basis.

I've been writing various GLSL functions with my current setup, and the center variable is loosely defined and may output a set of points ranging from a
singular point (the sphere), a curve (the second surface), or a plane in 3-space, or a surface in 3-space.

So, thinking backward from uv2vector, to ensure continuity among separate surfaces through animation with a time variable t, I am unsure how to combine normals or directions or a vector field. Instead of using standard cartesian coordinates <1,0,0> as normal <0,1,0> as right <0,0,1> as up, I'm defining a function for normal then forming cross products to produce an orthonormal basis.

I've extended the above example with a few more sceenshots:

In these the center curve is more clearly seen. The normal would be a vector field of directions corresponding to each derivative. I'm attempting to keep this simple, yet it's getting complex quick. Since the outer surface's vertices are calculated from the point-wise basis, if I were to use a function for the initial shape of the surface, then a separate function to animate it, as creativity may permit, I'm lost as to how I might combine directions.

 

[ADDA]

yet I am unable to think or remember which operation I would use to combine normals, or directions of the surface, with the two two functions w2normal and t2normal.

Got a bit wordy here. I am referring to the directions of the center curve, seen in the above examples with the parabolic dots.

I'm trying to figure out functional composition applied to a vector field. At least I think that's the proper term. I think, perhaps...

f(w) = w2normal (initial vector field)
g(t) = t2normal (animated vector field)

To ensure continuity among surfaces I would need a different parametric function of w and t instead of separate functions. However, I would like to compose it of f(w) and g(t), so that I may write different g(t) functions for one f(w) function.

h(w,t) = ?

 

[ADDA]

Mark44, I guess all that I needed was the sum rule of derivatives... the gifs are not animating?

 

[ADDA]

There is a solution to surface continuity:

 

[ADDA]

End Result: