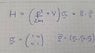How to diagonalize Hamiltonian with Zeeman field

Click For Summary

Discussion Overview

The discussion revolves around the diagonalization of a Hamiltonian for an electron in a Zeeman field, focusing on the coupling of the electron's spin to the magnetic field. Participants explore methods for setting up the Hamiltonian and solving for eigenvalues, considering both perturbative and exact approaches.

Discussion Character

  • Technical explanation, Debate/contested, Mathematical reasoning

Main Points Raised

  • One participant describes their approach to setting up the Hamiltonian, combining the kinetic and potential energy terms with the Zeeman term, but expresses uncertainty about solving the Hamiltonian.
  • Another participant suggests that the problem is typically solved using perturbation theory, referencing standard quantum mechanics textbooks.
  • A subsequent participant questions whether an exact analytical expression for the eigenenergies can be found, implying a desire for a more precise solution.
  • One participant proposes that a unitary transformation can be used to rotate the magnetic field to align with the z-axis, which would diagonalize the Hamiltonian, leaving only the sigma_z component.
  • A later reply reiterates the unitary transformation approach but notes that while it diagonalizes the interaction Hamiltonian, it does not necessarily diagonalize the full Hamiltonian.
  • Another participant asserts that if the magnetic field is constant, the transformation does diagonalize the Hamiltonian in spin space.

Areas of Agreement / Disagreement

Participants express differing views on the methods for diagonalizing the Hamiltonian, with some advocating for perturbative solutions and others for exact methods. The discussion remains unresolved regarding the best approach to take.

Contextual Notes

The discussion includes assumptions about the constancy of the magnetic field and the applicability of perturbation theory, which are not fully explored or agreed upon by participants.

aaaa202
Messages
1,144
Reaction score
2
Recently I have been asked to solve the problem of an electron in a Zeeman-field that couples the spin of the electron to the magnetic field.
I am not sure how to correctly set up the problem. I think, however, that what I have done on the picture is correct. The usual p^2/2m + V term in the Hamiltonian is tensored with the identity matrix and the Zeeman term is added in the usual way.
I am however unsure how to solve this Hamiltonian. How do you solve something like this with both an eigenvalue equation in the matrix structure and in the spatial part of H?
 

Attachments

  • 14202967_1391025530909502_1215176686_o.jpg
    14202967_1391025530909502_1215176686_o.jpg
    36.6 KB · Views: 766
Physics news on Phys.org
This is usually solved perturbatively. Most QM textbooks have a chapter on time-independent perturbation theory.
 
Okay but is it not possible to find the exact analytical expression for the eigenenergies?
 
Easy. Just find a unitary transformation which rotates B in the direction of the z axis. Then the hamiltonian will be diagonal as only the sigma_z component remains.
 
DrDu said:
Easy. Just find a unitary transformation which rotates B in the direction of the z axis. Then the hamiltonian will be diagonal as only the sigma_z component remains.
This diagonalizes the interaction Hamiltonian, but not the full Hamiltonian.
 
If B is constant, it does, at least in spin space.
 
  • Like
Likes   Reactions: Demystifier

Similar threads

Undergrad Derivation of normal Zeeman-Effect
  • · Replies 5 ·
Replies
5
Views
2K
Undergrad Questions on the classical interpretation of (normal) Zeeman effect
  • · Replies 10 ·
Replies
10
Views
2K
Undergrad Hamiltonian of a particle in a magnetic field
  • · Replies 10 ·
Replies
10
Views
4K
Undergrad Separable Hamiltonian for central potential
  • · Replies 21 ·
Replies
21
Views
3K
Undergrad Can an electron in a magnetic field radiate a virtual photon?
  • · Replies 3 ·
Replies
3
Views
2K
Undergrad Understanding the Effects of Parities on the Stark Hamiltonian
  • · Replies 1 ·
Replies
1
Views
1K
Undergrad Heisenberg Equations of Motion for Electron in EM-field
  • · Replies 9 ·
Replies
9
Views
2K
Undergrad Strange Hamiltonian of two particles on the surface of a sphere
  • · Replies 1 ·
Replies
1
Views
2K
Undergrad Scalar Hamiltonian and electromagnetic transitions
  • · Replies 5 ·
Replies
5
Views
1K
Undergrad Rabi Hamiltonian : counter-rotating terms
  • · Replies 2 ·
Replies
2
Views
2K