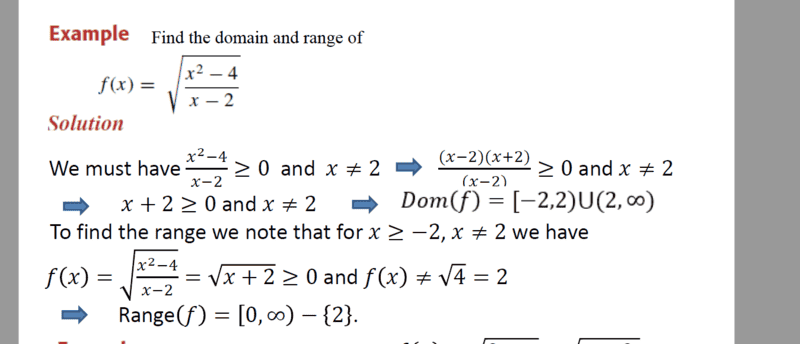SUMMARY
The discussion focuses on determining the range of the function f(x) = √(x + 2) for x ≠ 2. The function is established as monotonically increasing for the interval -2 < x < +∞, leading to the conclusion that the range is [0, ∞) excluding the value at x = 2, which results in f(2) = 2. The critical insight is that the square root function's increasing nature simplifies the determination of the range, as it is directly tied to the minimum and maximum values of the expression x + 2.
PREREQUISITES
- Understanding of square root functions
- Knowledge of function behavior and monotonicity
- Familiarity with domain and range concepts
- Basic algebraic manipulation skills
NEXT STEPS
- Study the properties of monotonically increasing functions
- Learn how to find the range of composite functions
- Explore the implications of domain restrictions on function behavior
- Investigate the graphical representation of square root functions
USEFUL FOR
Students studying algebra, particularly those struggling with understanding the range of functions, as well as educators seeking to clarify concepts related to square root functions and their properties.