Discussion Overview
The discussion revolves around calculating the relative error in voltage readings from a circuit with three resistors in series, specifically focusing on the impact of the voltmeter's internal resistance. The scope includes theoretical calculations and application of circuit analysis principles.
Discussion Character
- Homework-related
- Mathematical reasoning
- Technical explanation
- Debate/contested
Main Points Raised
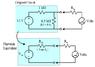
- One participant presents a formula for relative error (Er) as Er = - (Rs / (Rs + Rm)) * 100% but expresses uncertainty about the calculation of Rs.
- Another participant questions the definitions of Rs and Rm and the context of the formula, seeking clarification on what is being compared in the relative error calculation.
- A participant explains that the formula is derived from the voltage divider equation and provides definitions for Rs (source resistance) and Rm (meter resistance), emphasizing the context of measuring voltage across resistors.
- There is a request for a picture of the textbook page that presents the formula, indicating a need for verification of the equation's presentation.
- Discussion arises about the notation used in the formula, with a participant noting that the lack of parentheses can lead to misinterpretation of the equation.
- One participant suggests that the source resistance Rs is the output resistance seen by the meter and inquires if the original poster has studied Thevenin Equivalent Circuits.
- The original poster indicates they have not yet covered Thevenin Equivalent Circuits but are learning about series and parallel circuits and voltage measurements with digital voltmeters.
- A suggestion is made to use basic circuit analysis methods (KVL, KCL) to find the unloaded and loaded voltages to determine the percentage change.
Areas of Agreement / Disagreement
Participants express differing views on the correct application of the formula and the definitions of the variables involved. There is no consensus on the correct interpretation of the formula or the calculations presented.
Contextual Notes
There are uncertainties regarding the definitions of Rs and Rm, the correct application of the formula, and the implications of the notation used in the equation. Additionally, the discussion reflects a reliance on foundational circuit analysis concepts that may not have been fully covered by all participants.