5416339
- 18
- 0
This question is from a "Solved Problems" book where they give the solutions but I'm not able to get the reason !
Question :
ABCD is a quadrilateral.Force BA,BC,CD and DA act at a point.Their resultant is :
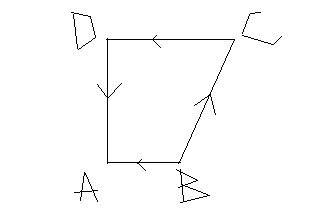
Options:
a. 2AB
b. 2DA
c. 2BC
d. 2BA
The given answer is : 2BA
Formulas Related
Polygonal Laws of vector which states that the resultant will be the Line joining the Initial point and the final point !
My Attempt:
How is this possible.I'm not able to understand how we should find the resultant of the Quadrilateral because AB is not joining "Head to Tail" and "Tail to Head" instead it is joining from "Tail to Tail" and "Head to Head" ! So how do i solve this please give a proper explanation for this !
What i think is that only "AB" is the answer because When we join the initial point "B" with the final point "D" we should get the resultant ! So how do we do this ?
Please help me Understand this ! Am i mixing up the concepts or what ?
Question :
ABCD is a quadrilateral.Force BA,BC,CD and DA act at a point.Their resultant is :
Options:
a. 2AB
b. 2DA
c. 2BC
d. 2BA
The given answer is : 2BA
Formulas Related
Polygonal Laws of vector which states that the resultant will be the Line joining the Initial point and the final point !
My Attempt:
How is this possible.I'm not able to understand how we should find the resultant of the Quadrilateral because AB is not joining "Head to Tail" and "Tail to Head" instead it is joining from "Tail to Tail" and "Head to Head" ! So how do i solve this please give a proper explanation for this !
What i think is that only "AB" is the answer because When we join the initial point "B" with the final point "D" we should get the resultant ! So how do we do this ?
Please help me Understand this ! Am i mixing up the concepts or what ?
Last edited: