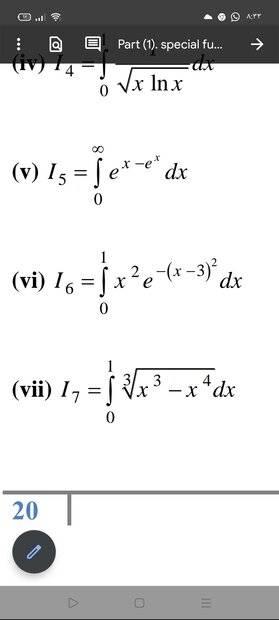SUMMARY
The discussion centers on fixing the limits of integration for the gamma integral I_6 = ∫_2^3 (3-y)² e^(-y²) dy to match the standard gamma function form. The user attempts to transform the integral using partial integration and expresses it in terms of incomplete gamma functions, which are not covered in their course. The conversation highlights the relationship between the incomplete gamma function and the error function, specifically γ(1/2, x) = √π erf(√x). Ultimately, the user seeks clarification on expressing the integral strictly in terms of the gamma function.
PREREQUISITES
- Understanding of gamma functions and their properties
- Familiarity with integration techniques, particularly partial integration
- Knowledge of the error function and its relation to the gamma function
- Basic calculus skills, including limits of integration
NEXT STEPS
- Study the properties of the incomplete gamma function and its applications
- Learn how to express integrals in terms of gamma functions
- Explore the relationship between the error function and the gamma function
- Practice solving integrals using partial integration techniques
USEFUL FOR
Students studying advanced calculus, particularly those focusing on gamma functions and their applications in integral calculus. This discussion is also beneficial for educators seeking to clarify the relationship between different mathematical functions.