How to Formulate Circuit Analysis Equations into Matrix Form?

[VinnyCee]

Using superposition, find $v_0$ in the following circuit.

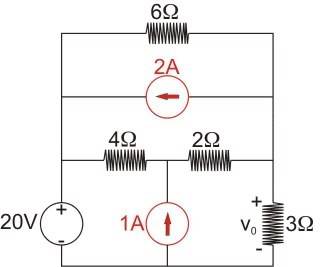
My work so far:

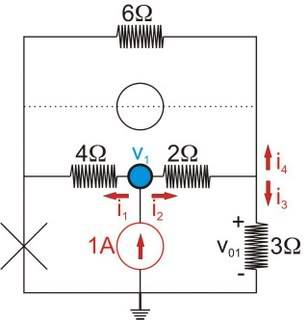
$$v_1\,=\,2\,i_2\,+\,v_{0\,1}$$

$$v_1\,=\,4\,i_1$$

$$v_{0\,1}\,=\,3\,i_3$$

$$v_{0\,1}\,=\,6\,i_4$$

KCL @ v1:
$$1\,A\,=\,i_1\,+\,i_2$$

$$i_2\,=\,i_3\,+\,i_4$$


Using these six equations, with 6 variables:

$$v_{0\,1}\,=\,\frac{12}{7}\,V$$

Is that correct?

My real question is how to put the six equations above into matrix form to enable solving using RREF.

Thanks

EDIT: I have fixed this part with Paallikko's guidance (thanks!)

$$i_1\,=\,\frac{1}{4}\,v_1$$

$$i_2\,=\,\frac{1}{2}\,v_1\,-\,\frac{1}{2}\,v_{01}$$

$$i_3\,=\,\frac{1}{3}\,v_{01}$$

$$i_4\,=\,\frac{1}{6}\,v_{01}$$

$$i_1\,+\,i_2\,=\,1\,A\,\,\,\Rightarrow\,\,\,\frac{3}{4}\,v_1\,-\,\frac{1}{2}\,v_{01}\,=\,1$$

$$i_3\,+\,i_4\,=\,i_2\,\,\,\Rightarrow\,\,\,\frac{1}{3}\,v_{01}\,+\,\frac{1}{6}\,v_{01}\,=\,\frac{1}{2}\,v_1\,-\,\frac{1}{2}\,v_{01}$$

$$v_{01}\,=\,1\,V$$

 

[VinnyCee]

Apply superposition two:

$$i_3\,=\,i_2\,-\,2\,A$$

$$i_1\,=\,i_0\,+\,i_2$$

$$v_{0\,2}\,=\,6\,i_1\,=\,6\,i_3\,=\,3\,i_o$$

From these five equations, I put into a matrix and solve.

$$v_{0\,2}\,=\,-6\,V$$


Next, I do the last superposition:

The circuit above can be simplified:

$$v_{0\,3}\,=\,3\,I$$

$$v_{0\,3}\,=\,3\,\left(\frac{20\,V}{3\,\ohm}\right)\,=\,20\,V$$

Total them up:

$$v_0\,=\,v_{0\,1}\,+\,v_{0\,2}\,+\,v_{0\,3}$$

$$v_0\,=\,\left(\frac{12}{7}\,V\right)\,+\,(-6\,V)\,+\,(20\,V)$$

$$v_0\,=\,15.7\,V$$

Does this look right? If not, please explain the errors and how to correct them. Thanks

 

[Päällikkö]

Well, you've understood how to use superposition (setting the sources to 0), you even seem to have most of the equations right*. However, all your calculations are wrong.

The first one in matrix form would be (solve for i_x from the first equations and substitute into the KCL equations):

$$\left[ {\begin{array}{*{20}c} {3/4} & { - 1/2} \\ { - 1/2} & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {V_1} \\ {V_2} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right]$$

* the two equations below are wrong
$$i_1=i_0 + i_2$$
$$v_{0\,3}\,=\,3\,\left(\frac{20\,V}{3\,\ohm}\right) \,=\,20\,V$$PS. If you're not familiar with PSpice, there's a free version available for download eg. here: http://www.electronics-lab.com/downloads/schematic/013/ you can quickly check if your answers are correct with it.
PPS. the topic's more engineering or introductory physics than advanced physics.

 

[VinnyCee]

For the first incorrect equation (in the 2nd part of problem), I see that all the currents are going out of the node. Does this mean that the actual equation is $$i_0\,+\,i_1\,+\,i_2\,=\,0$$?

In the third part of the problem, is the error becuase I didn't include both resistors in the I = equation?

$$v_{03}\,=\,3\,I$$

$$v_{03}\,=\,3\,\left(\frac{20\,V}{6\,\ohm}\right)\,=\,10\,V$$

Is that right now?

 

[Päällikkö]

Yep, they're right now.

 

[VinnyCee]

How do I solve the second part? I keep getting 0V for $$v_{02}$$.

I also used Pspice and got an 8V differential at the resistor for $$v_0$$.

$$v_0\,=\,v_{01}\,+\,v_{02}\,+\,v_{03}$$

$$v_0\,=\,1V\,+\,0V\,+\,10V\,=\,11V$$

This is 3V higher than Pspice reports though.

 

[Päällikkö]

You've written:
v₀₂ = 3i₀ = 6i₁ = 6i₃ (1)
i₂ - i₃ = 2 (2)
i₀ + i₁ + i₂ = 0 (3)

Substituting (2) into (3) (Eliminating i₂):
i₀ + i₁ + i₃ = -2

Substituting (1) into the above:
v₀₂(1/3 + 1/6 + 1/6) = -2

=> v₀₂ = -3 (V)