Why does amplifier sink power for Vout>0 and sources power for Vout<0?

[zenterix]

TL;DR Summary: How do we show that the dependent current source in a single-stage amplifier sinks power for $v_{\text{out}}>0$ and sources power for $v_{\text{out}}<0$

I am trying to solve a problem set from MIT OpenCourseWare's 6.002 "Circuits and Electronics" course.

There is a problem about amplifiers that I would like to discuss here.

Consider the following two amplifiers

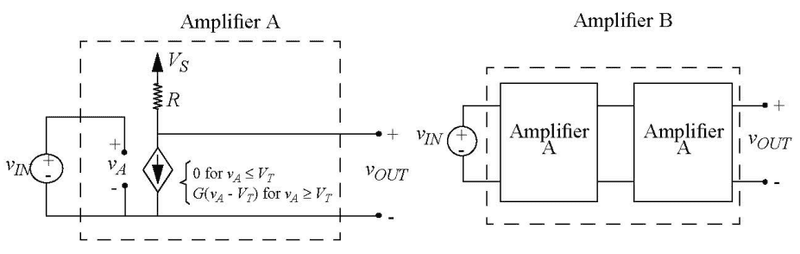
We are asked to show that the dependent current source sinks power for $v_{\text{out}}>0$ and sources power for $v_{\text{out}}<0$. I don't know how to do this.

There are a few questions before this one about the amplifers. In what follows, let me go through the calculations that they entailed.

Amplifier A is a single-state amplifier implemented with a voltage-dependent current source and pull-up resistor.

Let's assume that the current source parameters $G$ and $V_T$ satisfy $G>0$ and $V_S>V_T>0$. In addition, assume that $RG<\frac{V_S}{V_S-V_T}$.

Amplifier B is a two-stage amplifier in which each stage is identical to amplifier A.

The relationship between $v_{\text{out}}$ and $v_{in}$ for amplifier A can be obtained by applying KCL to the node with the positive terminal of $v_{\text{out}}$.

Assuming $v_{\text{in}}\geq V_T$,

$$\frac{V_S-v_{\text{out}}}{R}=G(v_{\text{in}}-V_T)^2\tag{1}$$

$$v_{\text{out}}=V_S-RG(v_{\text{in}}-V_T)^2\tag{2}$$

Graphically, this relationship looks like the light blue curve below

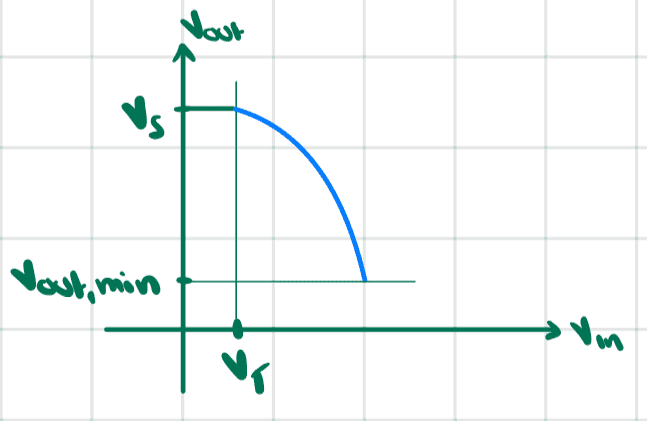
As $v_{\text{in}}$ increases, $v_{\text{out}}$ decreases until we have $v_{\text{out, min}}=v_{\text{in}}-V_T$.

$$v_{\text{out,min}}=V_S-RGv^2_{\text{out,min}}\tag{3}$$

which gives

$$v_{\text{out,min}}=\frac{-1+\sqrt{1+4RGV_S}}{2RG}\tag{4}$$

I'd like to determine $v_{\text{out}}$ as function of $v_{\text{in}}$ for amplifier B.

It seems that we have the following setup

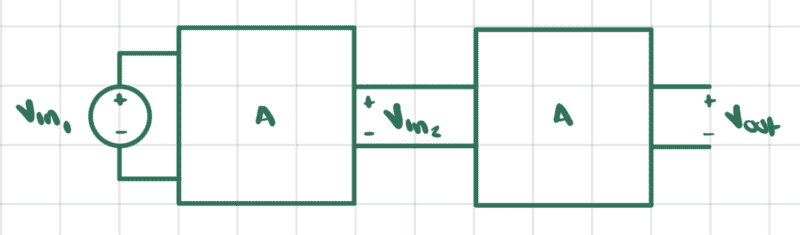
Assuming $v_{\text{in,1}}\geq V_T$ then

$$v_{\text{in,2}}=V_S-RG(v_{\text{in,1}}-V_T)^2\tag{5}$$

and assuming $v_{\text{in,2}}\geq V_T$ then

$$v_{\text{out}}=V_S-RG(v_{\text{in,2}}-V_T)^2\tag{6}$$

Subbing (5) into (6) we get

$$v_{\text{out}}=V_S-RG(V_S-V_T-RG(v_{\text{in,1}}-V_T)^2)^2\tag{7}$$

$$=(V_S-RG(V_S-V_T)^2)-2(RG)^2(V_S-V_T)(v_{\text{in,1}}-V_T)^2-(RG)^3(v_{\text{in,1}}-V_T)^4\tag{8}$$

This is the relationship between $v_{\text{out}}$ and $v_{\text{in}}$ for amplifier B.

We are asked to plot this relationship. I am still working on this.

Then there is the following question.

Consider amplifier A again. Show that the dependent current source sinks power for $v_{\text{out}}>0$ and sources power for $v_{\text{out}}<0$.

If $v_{\text{out}}$ is negative does this mean the voltage source is such that the positive terminal is now on the bottom and $v_{\text{in}}>V_S$?

 

[Baluncore]

We are asked to show that the dependent current source sinks power for Vout > 0 and sources power for Vout < 0. I don't know how to do this.

Power is the product of output current and voltage.
Sign is important in that it determines the direction of power flow.

You may not have realised that Vout,min can be negative.
That is the magic of ideal current sinks and sources.