How to Graph Potential Energy from Force Fx Along the x-axis?

[bestchemist]

1. Homework Statement

The figure shows the force Fx exerted on a particle that moves along the x-axis. Draw a graph of the particle's potential energy as a function of position x from 0m to 1.1m. Let U be zero at x=0m.

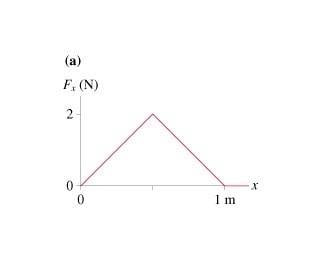
2. Homework Equations

W = F*d
U = mgh

 

[PhanthomJay]

Attempt please. Your relevant equations are not correct when the force is not constant. The force is not mg. Are you familiar with calculus or other means of calculating work or PE for non constant (assumed conservative) forces?

 

[bestchemist]

Attempt please. Your relevant equations are not correct when the force is not constant. The force is not mg. Are you familiar with calculus or other means of calculating work or PE for non constant (assumed conservative) forces?[/QUOT

Thank you for responding! :)

yeah... I'm not really good with Calculus...
IF those equation don't work then I think I have to use the following equation.

F = dU/dx
U = ∫F dx

but How do I integrate tho since the function of force is not given?

 

[voko]

How do I integrate tho since the function of force is not given?

It is given, via the diagram.

 

[bestchemist]

It is given, via the diagram.

since the slope from 0 to 0.5 is 4 then the force is F = 4x and the integral of that is 2x² right?
from 0.5 to 1 the force is what? since the slope there is -4, will it be F=-4x?

 

[PhanthomJay]

since the slope from 0 to 0.5 is 4 then the force is F = 4x and the integral of that is 2x² right?

yes, it is actually 2x^2 + k, where k is a constant, and since U =0 when x is 0, then k is 0, so U = 2x^2 between x = 0 and x = 0.5, an upward facing parabola

from 0.5 to 1 the force is what? since the slope there is -4, will it be F=-4x?

Not quite, are you familiar with the equation of a straight line , y = mx + b, where m is the slope of the line and b is the value of y at x = 0 (the y-intercept of the extended line)?

 

[bestchemist]

Not quite, are you familiar with the equation of a straight line , y = mx + b, where m is the slope of the line and b is the value of y at x = 0 (the y-intercept of the extended line)?

Soooo... From 0.5 to 1, F = -4x +4 since the force at 0.5 is 2 so the y intercept is 4!
And then the integral of F will be U=-(2x^2+4x +k) right??
But somehow when I graph this U graph... It doesn't look right. When I plug 0.6 in for x I got 3.12
I have a feeling that its wrong :( can someone please help.

 

[voko]

When you have $$ f(x) = \begin{cases} a(x), 0 \le x < 0.5 \\ b(x), 0.5 \le x < 1 \\ c(x) \end{cases} $$ then what is $$ \int_0^x f(x) dx $$?

 

[PhanthomJay]

Soooo... From 0.5 to 1, F = -4x +4 since the force at 0.5 is 2 so the y intercept is 4!

yes

And then the integral of F will be U=-(2x^2+4x +k) right??

you mean U = -2x^2 +4x + k, I think, where k can be found using the knowledge gained in the first part, U = 0.5 when x = 0.5, solve for k.

But somehow when I graph this U graph... It doesn't look right. When I plug 0.6 in for x I got 3.12

Try again, using the corrected equation for U.

Don't forget you then still need to graph the PE from x =1 to x = 1.1.

As a check of your calculus, remember that the area under the force-displacement curve from F=0 to F=x, is the PE at x.

I'm not so good at calculus, either, just the basics. Haven't used it much since college days.

 

[bestchemist]

When you have $$ f(x) = \begin{cases} a(x), 0 \le x < 0.5 \\ b(x), 0.5 \le x < 1 \\ c(x) \end{cases} $$ then what is $$ \int_0^x f(x) dx $$?

yes you mean U = -2x^2 +4x + k, I think, where k can be found using the knowledge gained in the first part, U = 0.5 when x = 0.5, solve for k. Try again, using the corrected equation for U.

Don't forget you then still need to graph the PE from x =1 to x = 1.1.

As a check of your calculus, remember that the area under the force-displacement curve from F=0 to F=x, is the PE at x.

I'm not so good at calculus, either, just the basics. Haven't used it much since college days.

Thank you guys,

I think I got it!

but for x=1 to x=1.1
isn't the force is zero so the PE is zero too? the slope is zero so F=0 integral of that will be zero too isn't it?

 

[voko]

but for x=1 to x=1.1
isn't the force is zero so the PE is zero too? the slope is zero so F=0 integral of that will be zero too isn't it?

Zero derivative does not mean that the function is zero. You want your potential energy to be a smooth function, so it should not be zero at x > 1 because it was not zero at x < 1.

 

[bestchemist]

Zero derivative does not mean that the function is zero. You want your potential energy to be a smooth function, so it should not be zero at x > 1 because it was not zero at x < 1.

Sooo
∫F= 0
so U = 0x +k
so U =1?

 

[voko]

Can you answer the question in #8?

 

[bestchemist]

Can you answer the question in #8?

nope :(
I got a(x) and b(x) but I don't know c(x)

 

[voko]

c(x) = 0, as given.

 

[bestchemist]

c(x) = 0, as given.

U = ∫₁^1.1 0
U= 0x + k
isn't it?

 

[voko]

$U = \int_{1}^{1.1} 0 dx$ has almost nothing to do with $U = \int_0^x f(x) dx$ as requested in #8. It cannot be the answer.

 

[bestchemist]

$U = \int_{1}^{1.1} 0 dx$ has almost nothing to do with $U = \int_0^x f(x) dx$ as requested in #8. It cannot be the answer.

I don't know what could it be then
I feel discourage :(
Can you tell me the answer and how you get it step by step, please...

 

[voko]

You need to find this: $$ U(x) = - \int_0^x f(x) dx $$ The complication is that $f(x)$ is not defined as a simple formula:
$$ f(x) = \begin{cases} a(x), 0 \le x < 0.5 \\ b(x), 0.5 \le x < 1 \\ c(x) \end{cases} $$

Obviously, when $0 \le x < 0.5$, you can say $U(x) = - \int_0^x a(x) dx$.

But when $x > 0.5$, you cannot say that $U(x) = \int_0^x a(x) dx$, nor can you say that $U(x) = \int_0^x b(x) dx$. However, for any $f(x)$ you can say $\int_0^x f(x) dx = \int_0^{0.5} f(x) dx + \int_{0.5}^x f(x) dx$, so, for $0.5 \le x < 1, \ U(x) = - \int_0^{0.5} a(x) dx - \int_{0.5}^x b(x) dx$.

Now you have to find $U(x)$ for $x \ge 1$.

 

[bestchemist]

You need to find this: $$ U(x) = - \int_0^x f(x) dx $$ The complication is that $f(x)$ is not defined as a simple formula:
$$ f(x) = \begin{cases} a(x), 0 \le x < 0.5 \\ b(x), 0.5 \le x < 1 \\ c(x) \end{cases} $$

Obviously, when $0 \le x < 0.5$, you can say $U(x) = - \int_0^x a(x) dx$.

But when $x > 0.5$, you cannot say that $U(x) = \int_0^x a(x) dx$, nor can you say that $U(x) = \int_0^x b(x) dx$. However, for any $f(x)$ you can say $\int_0^x f(x) dx = \int_0^{0.5} f(x) dx + \int_{0.5}^x f(x) dx$, so, for $0.5 \le x < 1, \ U(x) = - \int_0^{0.5} a(x) dx - \int_{0.5}^x b(x) dx$.

Now you have to find $U(x)$ for $x \ge 1$.

so for x>1
U(x) = -∫₀ ^0.5 ax dx - ∫_0.5 ¹ bx dx - ∫₁^x cx dx

right?

 

[voko]

so for x>1
U(x) = -∫₀ ^0.5 ax dx - ∫_0.5 ¹ bx dx - ∫₁^x cx dx

right?

Right!

 

[bestchemist]

Right!

Thank! Finally! let's me try to graph this thing and see it I get it right!
Thanks again! you're awesome!

 

[voko]

Just for the record, can you show your formulae for the potential energy in all the three intervals?

 

[bestchemist]

Just for the record, can you show your formulae for the potential energy in all the three intervals?

from 0<x<0.5
U = -2x²

from 0.5<x<1
U = -2x^2 +4x + k
k = -1
so U = -2x² +4x - 1

and for x >1

U(x) = -∫₀^0.5 ax dx - ∫_0.5¹ bx dx - ∫₁^x cx dx
U = - 2x<sup>2 - ( -2x2 +4x -1)
U = -4x + 1

Is it right?</sup>

 

[voko]

from 0<x<0.5
U = -2x²

Correct. So $\int_0^x a(x) dx = 2x^2$.

from 0.5<x<1
U = -2x^2 +4x + k
k = -1
so U = -2x² +4x - 1

This is supposed to be $- \int_0^{0.5} a(x) dx - \int_{0.5}^{x} b(x) dx$. From the above, $\int_0^{0.5} a(x) dx = 0.5$. What is $\int_{0.5}^{x} b(x) dx$?

and for x >1

U(x) = -∫₀^0.5 ax dx - ∫_0.5¹ bx dx - ∫₁^x cx dx
U = - 2x^{2 - ( -2x2 +4x -1)
U = -4x + 1}

<sup>You equate U with various different things here, so I am not sure I understand what you are saying here.

If $U = -4x + 1$ is the end result, it is wrong, because when $x > 1$, the force is zero, so the potential energy has to be constant.</sup>

 

[bestchemist]

Correct. So $\int_0^x a(x) dx = 2x^2$.



This is supposed to be $- \int_0^{0.5} a(x) dx - \int_{0.5}^{x} b(x) dx$. From the above, $\int_0^{0.5} a(x) dx = 0.5$. What is $\int_{0.5}^{x} b(x) dx$?



You equate U with various different things here, so I am not sure I understand what you are saying here.

If $U = -4x + 1$ is the end result, it is wrong, because when $x > 1$, the force is zero, so the potential energy has to be constant.

For x >0.5

U = -2x^2 - (-2x^2 +4x-1)
U = -4x +1

for X >1 since it is suppose to be constant

U = -4x +1 -(-4x+1)

I guess on this last one lol...Idk what should it be

 

[voko]

For x >0.5

U = -2x^2 - (-2x^2 +4x-1)
U = -4x +1

Why? I asked a specific question about $\int_{0.5}^{x} b(x) dx$. Answering it would be helpful for you.

 

[bestchemist]

Why? I asked a specific question about $\int_{0.5}^{x} b(x) dx$. Answering it would be helpful for you.

for x >0.5
F= -4x+4
so ∫f dx

U = - 2x^2 +4x +k

∫_0.5¹ -4x+4

isn't it?

 

[voko]

You are getting confused because you use the same letters to denote multiple things. Let $B(x) = \int_{0.5}^{x} b(x) dx$. What is $B(x)$, if $b(x) = -4x + 4$? What is $U(x)$, when $0.5 \le x < 1$?

 

[bestchemist]

You are getting confused because you use the same letters to denote multiple things. Let $B(x) = \int_{0.5}^{x} b(x) dx$. What is $B(x)$, if $b(x) = -4x + 4$? What is $U(x)$, when $0.5 \le x < 1$?

sooo
U = -2x^2 +4x +k ]^x - ( (-2x^2 +4x +k)]^0.5)

right?