colinbeaton1
- 10
- 0
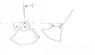
My goal is to fight the max amount of torque with the weight by having different densities at different places and by keeping the z center of mass low.
I need to find the answer out in terms of the three angles, and the final answer must not have a substituted angles such as 45 degrees.
I need an ideal density function in terms of x,y,z. In terms of height and radius from vertical axis.
The main function is the cone, and the details are here
http://www.wolframalpha.com/input/?i=cone+moment+of+inertia&lk=4&num=5&lk=4&num=5
At the bottom of the cone there is a spherical cap, details here
http://www.wolframalpha.com/input/?i=partial+sphere
Use mass m, and radius r, the angles, and the equations and please show me all the work so I can fully understand for later use.
I need to find the answer out in terms of the three angles, and the final answer must not have a substituted angles such as 45 degrees.
I need an ideal density function in terms of x,y,z. In terms of height and radius from vertical axis.
The main function is the cone, and the details are here
http://www.wolframalpha.com/input/?i=cone+moment+of+inertia&lk=4&num=5&lk=4&num=5
At the bottom of the cone there is a spherical cap, details here
http://www.wolframalpha.com/input/?i=partial+sphere
Use mass m, and radius r, the angles, and the equations and please show me all the work so I can fully understand for later use.