How to Solve Acceleration of Cart on 3 Different Slopes?

[LilRubyKinz]

Homework Statement

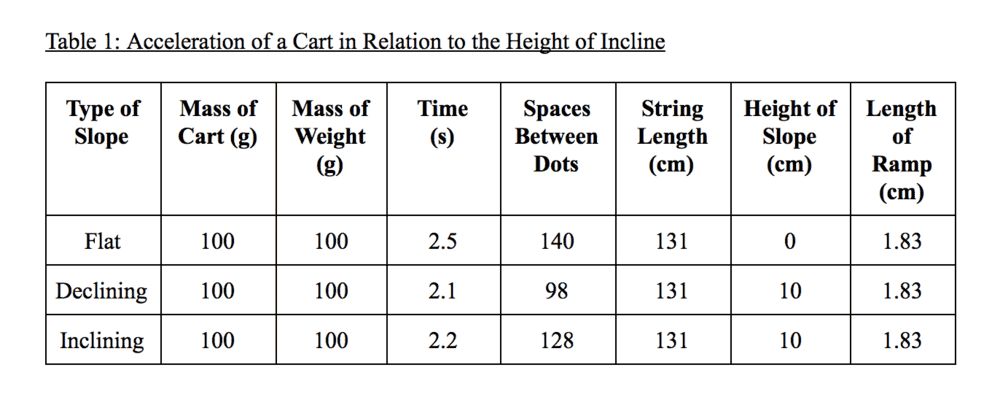
Lab Report - Perform experiment to find acceleration of a cart on three different types of slopes: Flat, Inclining, and Declining.

Relevant Equations

Type 1(Flat): a = m2g - (coefficient of friction)m1g / m1 + m2
Type 2(Inclining): a = T - (coefficient of friction) m1g(cos(theta)) - m1gsin(theta) / m1
Type 3(Declining): a = mg(sin(theta)) - (coefficient of friction)mg(cos(theta)) / m

I am trying to solve accelerations of a cart on these different slopes. I don't understand how it is possible without knowing the coefficient of friction, but my teacher says it is (very cryptically I might add). Can anyone help me understand this? Thanks.

 

[berkeman]

Welcome to the PF. Can you post some pictues or more information on the test setup? It's hard to help if we have to guess at your setup and what your data mean. Thanks.

 

[berkeman]

You can add pictures to a post / reply using the "attach a file" button.

 

[LilRubyKinz]

Thanks!

Yes, the experiment consists of a cart on a wooden ramp. The cart is attached to a ticker tape, which runs through the machine to get the period. The other end of the cart is attached to a string, which goes over a pulley and has a 100g weight hanging down. The cart is also 100g.

The first test is with the ramp laying flat. The second, the cart is going up the slope, with the third going down the slope.

With the measurements of the length of the base of the ramp and the height of the ramp's incline, we can get the angle.

Now, I have been trying to figure out how to solve acceleration without having the coefficient of friction. This is my hypothesis:

The coefficient of friction is a control between all experiments. Therefore, I can use the tan function of the right angle triangle to get the coefficient of friction. Is this true or am I completely wrong?

 

[LilRubyKinz]

 

[LilRubyKinz]

Those are some quick sketches to show how it is laid out.

 

[haruspex]

trying to solve accelerations

That, and your later comments, suggest you are trying to calculate what the acceleration should be in theory, whereas the measurements taken and your teacher's comments suggest you are only required to calculate what the three accelerations actually are. For the latter, you do not need to know the masses or the slope angle, or even the value of g. It's just a matter of assuming each acceleration is constant and calculating its value from the distance and time measurements.

You only give the whole times and distance. The mention of tickertape suggests you may have intermediate time and distance data too - do you?

 

[LilRubyKinz]

Okay, so what you're saying is that I can calculate the acceleration using the following instead of the circumstantial formulas he gave us?

Or should I use this to get acceleration, plug it into those formulas and find the coefficient of friction, then use that to solve the other accelerations?

 

[LilRubyKinz]

Okay, scratch that. This is what I'm doing now for each one using the results from the ticker tape. Does this format look correct?

The only thing is that my teacher says we will need to use trig ratios, which I haven't. Where am I supposed to use them?

 

[LilRubyKinz]

I'm really in need of help with this ASAP.

Another person suggested I make v a constant, measure tension with a Newton meter and solve for the coefficient... but I don't know how to do that? And where does period come into play?

 

[haruspex]

Okay, scratch that. This is what I'm doing now for each one using the results from the ticker tape. Does this format look correct?
...
The only thing is that my teacher says we will need to use trig ratios, which I haven't. Where am I supposed to use them?

are you saying it covered 140 dots in 2.5s? That gives an average speed of 56/s. But for acceleration you need the speed it reached in the 2.5s. Assume constant acceleration.

However, your trig ratios hint says you are expected to be applying some kinetic theory.
Your first and third relevant equations are correct except that you have omitted parentheses in the numerators and denominators of the divisions.
Your second equation is not useful in itself because you still have the unknown T in there. You need another equation involving T for the acceleration of the suspended mass. You can then combine these to eliminate T.

When you have done that you will have three equations in which the only unknowns are the three accelerations and coefficient of friction. So, yes, that is one too many unknowns to solve for. But then you can bring in the measured accelerations and instead have three equations with only one unknown. This means you will get three slightly different values for the coefficient.
What your teacher intends is not clear to me. I suspect she provided more guidance but you did not understand it. In the absence of clarification, I suggest you calculate the coefficient these three ways and compare the results.