Potatochip911
- 317
- 3
1. The problem statement, all variables and given/known }data
The picture I drew is quite sad but it's the best I could do lol.
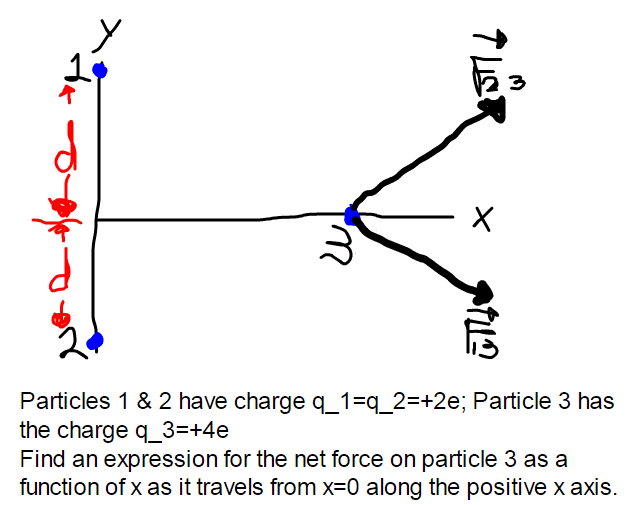
I forgot to mention in the image that it's the magnitude of the net force we're looking for.
##|F_{12}|=\frac{1}{4\pi\epsilon_0}\frac{|q_1||q_2|}{(R_{12})^2}##
I've tried solving it 2 ways and both have failed. The first method I tried was to ignore directional vectors since the y components cancel out in this example.
##F_{3}=F_{13}+F_{23}=\frac{1}{4\pi\epsilon_0}\frac{|q_1||q_3|}{(R_{13})^2}+\frac{1}{4\pi\epsilon_0}\frac{|q_2||q_3|}{(R_{23})^2}## ; Then since the hypotenuse of both triangles is the same we have ##R_{13}=R_{23}##; ##R_{13}=\sqrt{x^2+d^2}## and since ##q_1=q_2## we have $$F_{3}=\frac{1}{4\pi\epsilon_0}\frac{2|q_1||q_2|}{(R_{13})^2}=\frac{1}{4\pi\epsilon_0}\frac{2|q_1||q_2|}{x^2+d^2}$$
Unfortunately this isn't the correct expression, I also tried solving it with x and y components instead of magnitudes:
##F_3=\frac{1}{4\pi\epsilon_0}[\frac{|q_1||q_2|\cos\theta(+\hat{\imath})}{(R_{13})^2}+\frac{|q_1||q_2|\sin\theta(-\hat{\jmath})}{(R_{13})^2}]+\frac{1}{4\pi\epsilon_0}[\frac{|q_2||q_3|\cos\theta(+\hat{\imath})}{(R_{23})^2}+\frac{|q_2||q_3|\sin\theta(+\hat{\jmath})}{(R_{23})^2}]## which after simplifying leads to the expression $$F_3=\frac{1}{4\pi\epsilon_0}[\frac{2|q_1||q_3|\cos\theta}{(x^2+d^2)}]$$ which also isn't the correct expression even after substituting ##\cos\theta=\frac{x}{\sqrt{x^2+d^2}}##
The picture I drew is quite sad but it's the best I could do lol.
I forgot to mention in the image that it's the magnitude of the net force we're looking for.
Homework Equations
##|F_{12}|=\frac{1}{4\pi\epsilon_0}\frac{|q_1||q_2|}{(R_{12})^2}##
The Attempt at a Solution
I've tried solving it 2 ways and both have failed. The first method I tried was to ignore directional vectors since the y components cancel out in this example.
##F_{3}=F_{13}+F_{23}=\frac{1}{4\pi\epsilon_0}\frac{|q_1||q_3|}{(R_{13})^2}+\frac{1}{4\pi\epsilon_0}\frac{|q_2||q_3|}{(R_{23})^2}## ; Then since the hypotenuse of both triangles is the same we have ##R_{13}=R_{23}##; ##R_{13}=\sqrt{x^2+d^2}## and since ##q_1=q_2## we have $$F_{3}=\frac{1}{4\pi\epsilon_0}\frac{2|q_1||q_2|}{(R_{13})^2}=\frac{1}{4\pi\epsilon_0}\frac{2|q_1||q_2|}{x^2+d^2}$$
Unfortunately this isn't the correct expression, I also tried solving it with x and y components instead of magnitudes:
##F_3=\frac{1}{4\pi\epsilon_0}[\frac{|q_1||q_2|\cos\theta(+\hat{\imath})}{(R_{13})^2}+\frac{|q_1||q_2|\sin\theta(-\hat{\jmath})}{(R_{13})^2}]+\frac{1}{4\pi\epsilon_0}[\frac{|q_2||q_3|\cos\theta(+\hat{\imath})}{(R_{23})^2}+\frac{|q_2||q_3|\sin\theta(+\hat{\jmath})}{(R_{23})^2}]## which after simplifying leads to the expression $$F_3=\frac{1}{4\pi\epsilon_0}[\frac{2|q_1||q_3|\cos\theta}{(x^2+d^2)}]$$ which also isn't the correct expression even after substituting ##\cos\theta=\frac{x}{\sqrt{x^2+d^2}}##