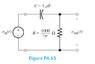
Discussion Overview
The discussion revolves around identifying and understanding high pass and low pass filters, specifically focusing on circuit diagrams and their characteristics. Participants explore the theoretical and practical aspects of second-order RLC circuits, including how to determine the type of filter based on circuit configuration and component behavior at varying frequencies.
Discussion Character
- Exploratory
- Technical explanation
- Conceptual clarification
- Debate/contested
- Homework-related
- Mathematical reasoning
Main Points Raised
- One participant requests help in drawing a circuit diagram for a second-order high pass filter and expresses confusion about identifying filter types from diagrams.
- Another participant explains the relationship between output voltage and the impedance of the capacitor and resistor, noting how frequency affects these impedances.
- Some participants discuss the behavior of capacitors at high and low frequencies, suggesting that this behavior helps classify filters as high or low pass.
- There is a proposal that reversing the order of components in a circuit changes the filter type, with specific examples given for high and low pass filters.
- A participant questions the definitions of "high pass" and "low pass," indicating a need for clarification on these terms.
- Discussion includes the implications of adding an inductor to a high pass filter circuit and how it affects the overall filtering characteristics.
- Some participants express uncertainty about whether certain configurations can be classified strictly as high or low pass filters, especially when output voltages do not equal input voltages at all frequencies.
- There is a mention of using transfer functions to classify filters, with a request for clarification on the values that would indicate high or low pass characteristics.
Areas of Agreement / Disagreement
Participants express various viewpoints on how to classify filters based on circuit configurations and component behavior. There is no consensus on whether certain circuits can be classified strictly as high or low pass, with some arguing that specific configurations may not fit neatly into either category.
Contextual Notes
Participants highlight limitations in understanding the definitions of filter types and the implications of circuit configurations on filtering behavior. There are unresolved questions regarding the classification of certain circuits and the behavior of output voltages in relation to input voltages across different frequencies.
Who May Find This Useful
Readers interested in circuit design, filter theory, and the analysis of RLC circuits may find this discussion beneficial for understanding the nuances of high and low pass filters.