Aerodin
- 5
- 0
[SOLVED] HW: Newton's Second Law and Angles
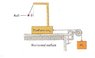
The system shown in the figure can be used to measure the acceleration of the system. An observer riding on the platform measures the angle (theta) that the thread supporting the light all makes with the vertical. There is no friction anywhere.
How is (theta) related to the acceleration of the system? (Mathematical/with an equation)
F=ma
Well, after working on this for at least an hour, I'm thinking that to figure out what the angle has to be I have to use the idea of drawing a free body diagram of the ball/angle part of the diagram or something. I'm really having some serious trouble doing this so any help would be awesome. Thanks!
Edit: I just figured out that if I do draw the whole free body diagram, it looks like i may be able to find how the angle is related. However, in order to do so, I need to know what the tension force of the string that the ball is on would be, and that's where I'm getting stuck.
Homework Statement
The system shown in the figure can be used to measure the acceleration of the system. An observer riding on the platform measures the angle (theta) that the thread supporting the light all makes with the vertical. There is no friction anywhere.
How is (theta) related to the acceleration of the system? (Mathematical/with an equation)
Homework Equations
F=ma
The Attempt at a Solution
Well, after working on this for at least an hour, I'm thinking that to figure out what the angle has to be I have to use the idea of drawing a free body diagram of the ball/angle part of the diagram or something. I'm really having some serious trouble doing this so any help would be awesome. Thanks!
Edit: I just figured out that if I do draw the whole free body diagram, it looks like i may be able to find how the angle is related. However, in order to do so, I need to know what the tension force of the string that the ball is on would be, and that's where I'm getting stuck.
Attachments
Last edited: