Hydraulic lifting force of this arrangement of pipes

[ucody0911]

Homework Statement

hydraulic lifting

Relevant Equations

pascal

Hello All, :)

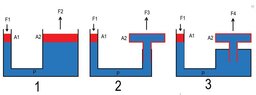
Please see the picture , input force F1 and area A1 and second area A2 are all same for 3 cases .
in case 2 and 3 , red open outline represents a free-to-move , ie , "T" piece move upward
for the 1st case , output force F2 should be F2=A2/A1 x F1 , by pascal's principle ,
what about output forces of F3 and F4 ? can be same as F2 ? how i calculate them ?

thanks

 

[Halc]

For F3 and F4, one must include the force downward on the red outline in the diagrams that have regions of fluid above the red parts.

 

[Lnewqban]

Work in = Work out
Force in x Delta height in = Force out x Delta height out

Piston diameter x Delta height = Displaced volume

Displaced volume in = Displaced volume out
Piston diameter in x Delta height in = Piston diameter out x Delta height out

Note that the top volume of the T shape does not change as the machine operates.

 

[ucody0911]

T piece is just hollow piston , therefore hydraulic pushing force exerted on upper side of T piston which has top area of A2

 

[jbriggs444]

T piece is just hollow piston , therefore hydraulic pushing force exerted on upper side of T piston which has top area of A2

And a bottom area nearly as great.

 

[Lnewqban]

T piece is just hollow piston , therefore hydraulic pushing force exerted on upper side of T piston which has top area of A2

Correct.
But that hydraulic pushing force exerted on upper side of hollow T piston, which has top area of A2, can't do any work.
The T-shaped piston is a single piece which surfaces can't move respect to each other (just like it happens to a pressurized gas tank).
The sliding telescopic portion, which cross section has a smaller area than the top surface A2, can move and do the lifting work.

 

[ucody0911]

so then what is the amount of force F2 and F3 ?

 

[haruspex]

so then what is the amount of force F2 and F3 ?

Post #3 gives you the easy way to solve these.
Consider how much the right hand top surface rises for a given depression of the left hand top surface.

 

[ucody0911]

consider , left side depression and right side rises are same for all 3 cases , and A2/A1 = 4 , F1 =100 N
then F2 will be 400 N for 1 st case .
F3 and F4 will same as 400 N ?

 

[haruspex]

left side depression and right side rises are same for all 3 cases

No.
If LHS goes down x, what volume flows across to the RHS?
If RHS goes up y, what extra volume is there on the RHS in each case?

 

[ucody0911]

No.
If LHS goes down x, what volume flows across to the RHS?
If RHS goes up y, what extra volume is there on the RHS in each case?

of course , RHS upwards forces depends volume flows and LHS depressions
i just wanted clarify that those F2 , F3 and F4 forces are equal like hydrostatic forces of previous talked subject .
Replied as all 3 hydrostatic forces are equal,
now here in this case , downward hydrostatic pressure replaced by upward hydraulic pressure , same in principal , therefore i thought that F2, F3 , F4 are equal,
if not equal , why ?

 

[haruspex]

if not equal , why ?

For the same reason that F1 and F2 are not equal. The hydrostatic pressures are equal there, but the forces are different because the pressure acts over different areas.

To avoid the complication introduced by the varying cross sections on the right hand sides, the easiest way is to think about work done when there is a small vertical displacement. In figure 1, if the LHS moves down x, it displaces volume xA1. So that much fluid flows to the right. How much will the RHS rise? Since the work done must be the same each side, how high does the RHS rise?

Apply the same analysis to the other diagrams.