Hydrodynamic drag of a rotating paddle wheel

[erlend]

Hello, i have a problem that look's easy to solve but really is not.

It involves a rotating paddle wheel submerged in water and i want to know the force exerted on the wheels and the torque required to rotate it. I have made a simple drawing to illustrate the problem below. I want to use the Drag equation to solve it, even though it is for linear motion, we can convert rotational motion to linear. But since the diameter changes the speed at any radial location and the force is based on a square function i can't get an exact solution for the problem.

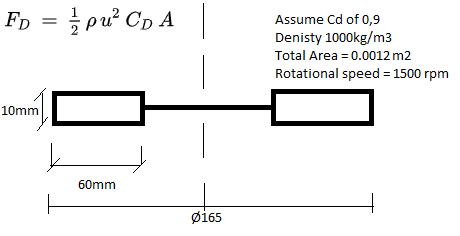
Can you help me with this problem?

 

[anorlunda]

This sounds like homework. Is it?

 

[erlend]

Hi anorlunda.

Actually this is not a homework problem.

I want to reduce the drag of something that is rotating in water and want to know the exact solution to it, i already have a rough estimate that would suffice for basic engineering. Just curious i quess :)

 

[erlend]

My current solution:
I assume the average speed to be in the middle of the paddle wheel. That point is located at Ø135 or r=0.0675M

v= r x RPM x rad/s
v =0.0675m x 1500rpm x 0.10472 = 10.6 meter / second

Drag equation using the speed:

So the combined torque for both sides of the paddle wheel would be:
Nm= 60 Newton * 0,0675M = 4.1 Nm

 

[Dr.D]

Why not set up the differential drag on a differential[ length and then integrate? But isn't the thing you want actually the total moment?

 

[erlend]

Hi Dr.D.

Yes i think you are correct that this is a calculus problem. If i replace v with r x RPM x rad/s in the drag equation, i could maybe setup an differential equation? The total moment is what I am after, i need to know the torque for selecting an electric motor.

 

[Chestermiller]

Hi Dr.D.

Yes i think you are correct that this is a calculus problem. If i replace v with r x RPM x rad/s in the drag equation, i could maybe setup an differential equation? The total moment is what I am after, i need to know the torque for selecting an electric motor.

Let's see your attempt to do this.

 

[Dr.D]

Its not hard. Just look at the force on a differential length, calculate the moment of that force, and then integrate to get the total moment.